Question

对于气温，通常有摄氏温度和华氏温度两种表示，且两者之间存在着某种函数关系，下列给出了摄氏（℃）温度x与华氏（℉）温度y之间对应关系．

x（℃）	…	-10	0	10	20	30	…
y（℉）	…	14	32	50	68	86	…

（1）通过①描点、连线；②猜想；③求解；④验证等几个步骤，试确定y与x之间的函数关系式；
（2）某天，沈阳的最高气温是12℃，台湾台北的最高气温是88℉，问这一天台北的最高气温比沈阳的最高气温高多少摄氏度（结果保留整数）

Answer 1

分析：（1）描点、连线即可作图，由图象可猜想y是x的一次函数，利用其中两点求出解析式，再把剩下的点代入，即可验证；
（2）令y=88，求出x，然后与12℃比较即可．

解答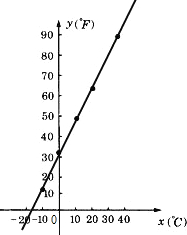：解：
（1）①如图：
②猜想：y是x的一次函数（3分）
③设y=kx+b
∵过点（0，32），（10，50）
∴

32=b 50=10k+b

∴

k=1.8 b=32

∴y=1.8x+32（4分）
④将其余三对数值分别代入③中的式子，结果等式均成立
∴y与x的关系式成立（6分）

（2）当y=88时，88=1.8x+32
∴x≈31，
∴31-12=19℃
答：这一天台北的最高气温比沈阳约高19℃．（8分）

点评：本题只需仔细分析图象，利用待定系数法即可求出解析式，从而解决问题．