题目内容
(本题10分) 已知一次函数y=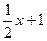 的图象与x轴交于点A.与
的图象与x轴交于点A.与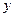 轴交于点
轴交于点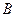 ;二次函数
;二次函数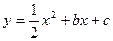 图象与一次函数y=
图象与一次函数y=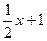 的图象交于
的图象交于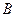 、
、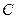 两点,与
两点,与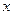 轴交于
轴交于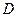 、
、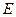 两点且
两点且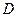 的坐标为
的坐标为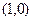
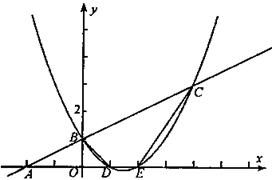
(1)求二次函数的解析式;
(2)在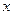 轴上是否存在点P,使得△
轴上是否存在点P,使得△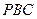 是直角三角形?若存在,求出所有的点
是直角三角形?若存在,求出所有的点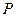 ,若不存在,请说明理由。
,若不存在,请说明理由。
 | |||||
 | |||||
 | |||||
解:(1)∵ 由题意知:当x=0时,y="1," ∴B(0,1), …………1分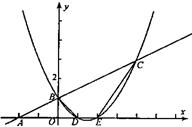
由 点的坐标为
点的坐标为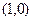 当x=1时, y=0
当x=1时, y=0
∴ 解得
解得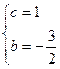 ,…………3分
,…………3分
所以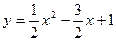 …………4分
…………4分
(2)存在;设P(a,0),
①P为直角顶点时,如图,过C作CF⊥x轴于F, ∵Rt△BOP∽Rt△PFC,
由题意得,AD=6,OD=1,易知,AD∥BE,
∴ .即
.即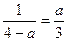 , …………5分
, …………5分
整理得:a2-4a+3=0,解得a=1或a="3, "
此时所求P点坐标为(1,0)或(3,0). …………7分
②若B为直角顶点,则有PB²+BC²=PC²
既有 1²+a²+4²+2²=3²+(4-a) ²
解得 a=0.5此时所求P点坐标为(0.5,0) ……8分
③若C为直角顶点,则有PC²+BC²=PB²
既有 3²+(4-a) ² +4²+2²=1²+a²
解得 a=5.5此时所求P点坐标为(5.5,0) ……9分
综上所述,满足条件的点P有四个,分别是(1,0)(3,0)(0.5,0) (5.5,0)。……10分
解析

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 ,并写出△
,并写出△
 C=90°,以AB为直径的OM交OC于点D、E,连结AD、BD.现以O为坐标原点,OA、OC所在直线为x轴、y轴建立如图所示直角坐标系,若抛
C=90°,以AB为直径的OM交OC于点D、E,连结AD、BD.现以O为坐标原点,OA、OC所在直线为x轴、y轴建立如图所示直角坐标系,若抛 物线y=ax2-2ax-3a(a<0)经过点A、B、D,且B为抛物线的顶点.
物线y=ax2-2ax-3a(a<0)经过点A、B、D,且B为抛物线的顶点.
