题目内容
若a、b 是正数,a-b=l,ab=2,则a+b=
- A.-3
- B.3
- C.±3
- D.9
B
分析:根据(a+b)2=(a-b)2+4ab,代值计算,再开平方求解.注意若a、b 是正数,则a+b>0.
解答:∵(a+b)2=(a-b)2+4ab=12+4×2=9,
开平方,得a+b=±3,
又∵a、b 是正数,
∴a+b>0,
∴a+b=3.
故选B.
点评:本题考查了完全平方公式,熟记公式的几个变形公式对解题大有帮助.
分析:根据(a+b)2=(a-b)2+4ab,代值计算,再开平方求解.注意若a、b 是正数,则a+b>0.
解答:∵(a+b)2=(a-b)2+4ab=12+4×2=9,
开平方,得a+b=±3,
又∵a、b 是正数,
∴a+b>0,
∴a+b=3.
故选B.
点评:本题考查了完全平方公式,熟记公式的几个变形公式对解题大有帮助.

练习册系列答案
相关题目
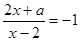 的解是正数,求a的取值范围 .
的解是正数,求a的取值范围 .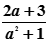 的值是正数,则a的取值范围是
的值是正数,则a的取值范围是