题目内容
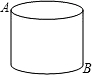
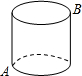如图，在底面周长为6，高为4的圆柱体上有A、B两点，则A、B最短矩离为（ ）A、2
| ||
| B、52 | ||
| C、10 | ||
| D、5 |
分析：要求圆柱体上两点之间的最短路径，最直接的作法，就是将圆柱体展开，然后利用两点之间线段最短解答．
解答：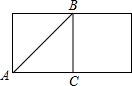
解：如图将圆柱体展开，根据“两点之间，线段最短”知，线段AB即为最短路线．
A、B最短矩离=
=
=5．
故选D．
解：如图将圆柱体展开，根据“两点之间，线段最短”知，线段AB即为最短路线．A、B最短矩离=
| AC2+BC2 |
| 32+42 |
故选D．
点评：考查了平面展开-最短路径问题，将圆柱体侧面展开为长方形，根据两点之间，线段最短，由勾股定理即可求解．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南师范大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
如图，在底面周长为6，高为4的圆柱体上有A、B两点，则A、B最短矩离为
