题目内容
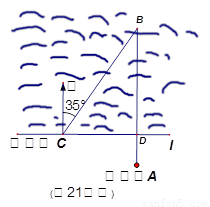
某海滨浴场东西走向的海岸线可以近似看作直线l(如图).救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号,他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙.乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东35°方向,甲乙的游泳速度都是2米/秒.问谁先到达B处?请说明理由.
(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
【答案】
由题意得∠BCD=55°,∠BDC=90°
∵tan∠BCD=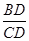
∴BD=CD·tan∠BCD=40×tan55°≈57.2(米)
∵ cos∠BCD=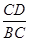
∴BC=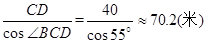 (5分)
(5分)
∴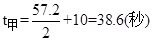
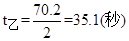 (7分)
(7分)
∴t甲>t乙
答:乙先到达B处。(9分)
【解析】在直角△CDB中,利用三角函数即可求得BC,BD的长,则求得甲、乙的时间,比较二者之间的大小即可.

练习册系列答案
相关题目
 (2012•温州)某海滨浴场东西走向的海岸线可近似看作直线l(如图).救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号.他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙.乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东35°方向,甲、乙的游泳速度都是2米/秒.问谁先到达B处?请说明理由.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
(2012•温州)某海滨浴场东西走向的海岸线可近似看作直线l(如图).救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号.他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙.乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东35°方向,甲、乙的游泳速度都是2米/秒.问谁先到达B处?请说明理由.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43) . 救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号. 他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙. 乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东
. 救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号. 他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙. 乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东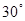 方向,甲、乙的游泳速度均是2米/秒.问谁先到达B处?请说明理由.
方向,甲、乙的游泳速度均是2米/秒.问谁先到达B处?请说明理由.
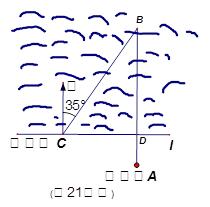
 . 救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号. 他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙. 乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东
. 救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号. 他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙. 乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东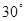 方向,甲、乙的游泳速度均是2米/秒.问谁先到达B处?请说明理由.
方向,甲、乙的游泳速度均是2米/秒.问谁先到达B处?请说明理由.