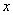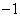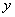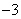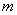题目内容
已知:二次函数
 中的
中的 满足下表:
满足下表:
|
|
|
|
0 |
1 |
2 |
3 |
|
|
|
|
0 |
|
|
|
|
|
(1)求 的值;
的值;
(2)根据上表求 时的
时的 的取值范围;
的取值范围;
(3)若 ,
, 两点都在该函数图象上,且
两点都在该函数图象上,且 ,试比较
,试比较 与
与 的大小.
的大小.
【答案】
(1) ;(2)
;(2)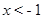 或
或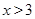 ;(3)
;(3)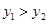
【解析】
试题分析:(1)根据表中数据可得抛物线的对称轴为x=1,再根据抛物线的对称性求解即可;
(2)根据表中的数据特征结合二次函数的性质即可作出判断;
(3)由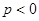 可得
可得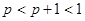 ,再结合抛物线的对称轴为
,再结合抛物线的对称轴为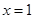 即可作出判断.
即可作出判断.
(1)由题意得 ;
;
(2)由题意得当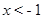 或
或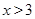 时,
时,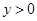 ;
;
(3)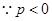 ,
,
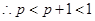
又∵抛物开口向上,对称轴为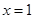 ,
,
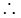
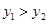 .
.
考点:二次函数的性质
点评:二次函数的性质是初中数学的重点,是中考常见题,一般难度不大,需熟练掌握.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目



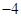
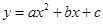
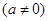 中的
中的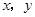 满足下表:
满足下表: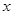


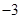
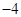
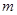
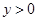 时的
时的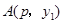 ,
, 两点都在该函数图象上,且
两点都在该函数图象上,且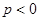 ,试比较
,试比较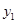 与
与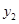 的大小.
的大小.  中的x、y满足下表:
中的x、y满足下表: