Question

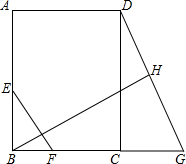已知：如图，矩形ABCD中，点G为BC延长线上一点，连接DG，BH⊥DG于H，且GH=DH，点E，F分别在AB，BC上，且EF∥DG．
（1）若AD=3，CG=2，求DG的长；
（2）若GF=AD+BF，求证：EF=

1

2

DG．

Answer 1

分析：（1）判断△BHG∽△DCG通过AD=3，CG=2，GH=DH，即可求DG的长；
（2）由GF=AD+BF，AD=BG，经过线段代换易得GC=2BF，再由EF∥DG得到∠BFE=∠CGD，根据三角形相似的判定易得Rt△BEF∽Rt△GDC，利用相似比即可得到结论．

解答：解：（1）在△BHG与△DCG中，
∵∠BGH=∠DGC，BH⊥DG，DC⊥BG，
∴∠BHG=∠DCG=90°，
∴△BHG∽△DCG，
∵AD=3，CG=2，BG=5，GH=DH，
∴

CG

HG

=

DG

BG

，
∴DG=2

5

，
即DG的长为2

5

；

（2）证明：∵GF=AD+BF，
∴FC+GC=BF+FC+BF，即GC=2BF，
∵EF∥DC，
∴∠BFE=∠GCD
∴Rt△BEF∽Rt△GDC，
∴EF：DG=BF：GC=1：2，
∴EF=

1

2

DG．

点评：本题考查了直角梯形的性质：有一组对边平行，另一组对边不平行，且有一个直角．也考查了矩形的性质、勾股定理、等腰三角形的判定以及相似三角形的判定与性质．