题目内容
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

【答案】(1)证明见解析;(2)70°.
【解析】试题分析:(1)应用“边角边”证得△BDE≌△CEF,所以DE=EF,即△DEF是等腰三角形;
(2)应用角的和差和三角形外角的性质可得∠DEF+∠CEF=∠B+∠BDE ,由△BDE≌△CEF可得∠BDE=∠CEF,进而证得∠DEF=∠B,在△ABC中求得∠B的度数,即可得到∠DEF的度数.
试题解析:(1)证明:∵AB=AC,∴∠B=∠C,
在△BDE和△CEF中:
∵BD=CE,∠B=∠C,BE=CF,
∴△BDE≌△CEF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
(2)解:∵∠DEC=∠B+∠BDE,
即∠DEF+∠CEF=∠B+∠BDE ,
由(1)知△BDE≌△CEF,
则∠BDE=∠CEF,
∴∠DEF=∠B,
∵∠A=40°,
∴∠B=∠C=![]() =70°,
=70°,
∴∠DEF=70°.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
【题目】如图所示,是一列用若干根火柴棒摆成的由正方形组成的图案.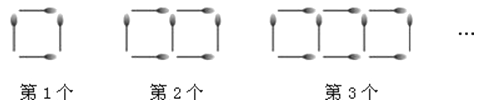
(1)完成下表的填空:
正方形个数 | 1 | 2 | 3 | 4 | 5 | 6 | n |
火柴棒根数 | 4 | 7 | 10 | 13 |
(2)某同学用若干根火柴棒按如上图列的方式摆图案,摆完了第1个后,摆第2个,接着摆第3个,第4个,…,当他摆完第n个图案时剩下了20根火柴棒,要刚好摆完第n+1个图案还差2根.问最后摆的图案是第几个图案?