题目内容
若正整数k满足个位数字为1，其他数位上的数字均不为1且十位与百位上的数字相等，
我们称这样的数k为“言唯一数”，交换其首位与个位的数字得到一个新数k'，并记F（k）=
．
（1）最大的四位“言唯一数”是 ，最小的三位“言唯一数”是 ；
（2）证明：对于任意的四位“言唯一数”m，m+m'能被11整除；
（3）设四位“言唯一数”n=1000x+100y+10y+1（2≤x≤9，0≤y≤9且y≠1，x、y均为整数），若F（n）仍然为“言唯一数”，求所有满足条件的四位“言唯一数”n．
练习册系列答案
相关题目
米，此时水位上升了多少米？
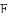
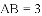
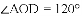
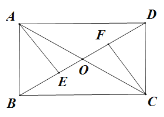
，则
___________．