题目内容
我们把能平分四边形面积的直线称为“好线”.利用下面的作图,可以得到四边形的“好线”:
(1)如图(1),在四边形ABCD中,BD为其中一条对角线,请你用尺规作图的方法找出BD的中点O;
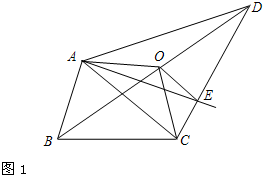
(2)如图(2),在四边形ABCD中,对角线BD的中点为O,连结OA、OC.显然,折线AOC能平分四边形ABCD的面积,再过点O作OE∥AC交CD于E,则直线AE即为一条“好线”.试说明直线AE是“好线”的理由;
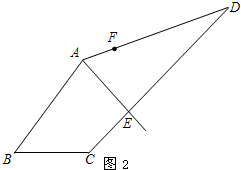
(3)如图(3),AE为四边形ABCD一条“好线”,F为AD边上的一点,请作出经过F点的“好线”,并对画图作适当说明(不需要说明理由).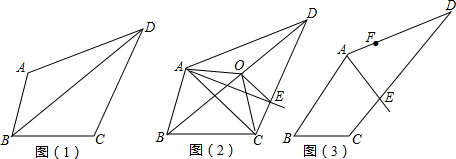
(1)如图(1),在四边形ABCD中,BD为其中一条对角线,请你用尺规作图的方法找出BD的中点O;
(2)如图(2),在四边形ABCD中,对角线BD的中点为O,连结OA、OC.显然,折线AOC能平分四边形ABCD的面积,再过点O作OE∥AC交CD于E,则直线AE即为一条“好线”.试说明直线AE是“好线”的理由;
(3)如图(3),AE为四边形ABCD一条“好线”,F为AD边上的一点,请作出经过F点的“好线”,并对画图作适当说明(不需要说明理由).

分析:(1)分别以B、D为圆心,以大于
BD为半径作圆,两圆交于E、F,作直线EF交BD于O,则O为BD的中点.
(2)根据等底等高的三角形面积相等得出△ACO的面积和△AEC面积相等,推出△AMO的面积=△CME的面积,即可得出答案.
(3)连接EF,过A作EF的平行线交CD于M,作直线FM即可.
| 1 |
| 2 |
(2)根据等底等高的三角形面积相等得出△ACO的面积和△AEC面积相等,推出△AMO的面积=△CME的面积,即可得出答案.
(3)连接EF,过A作EF的平行线交CD于M,作直线FM即可.
解答:解:(1)如图(1)点O为BD的中点;
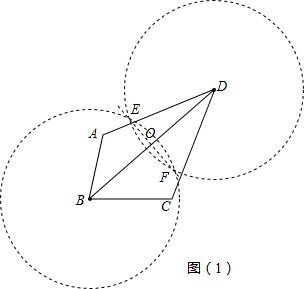 .
.
(2)
理由是:∵AC∥OE,
∴△AOC的边AC上的高和△AEC的边AC上的高相等,
∴S△AOC=S△AEC,
∴S△AOC-S△AMC=S△AEC-S△AMC,
∴S△AMO=S△CME,
∵折线AOC是“好线”,
∴S四边形AMCB+S△AMO=S△CME+S四边形DOME+S△AOD,
∴S四边形AECB=S△AED,
(3)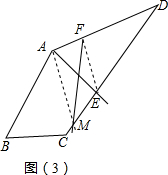
连接EF,过A作AM∥EF,交CD于M,作直线FM,
则直线FM为“好线”.
 .
.(2)

理由是:∵AC∥OE,
∴△AOC的边AC上的高和△AEC的边AC上的高相等,
∴S△AOC=S△AEC,
∴S△AOC-S△AMC=S△AEC-S△AMC,
∴S△AMO=S△CME,
∵折线AOC是“好线”,
∴S四边形AMCB+S△AMO=S△CME+S四边形DOME+S△AOD,
∴S四边形AECB=S△AED,
(3)

连接EF,过A作AM∥EF,交CD于M,作直线FM,
则直线FM为“好线”.
点评:本题考查了三角形的面积,平行线之间的距离的应用,注意:等底等高的三角形面积相等.

练习册系列答案
相关题目