题目内容
【题目】如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线![]() 过点A(—1,0),与⊙C相切于点D,
过点A(—1,0),与⊙C相切于点D,
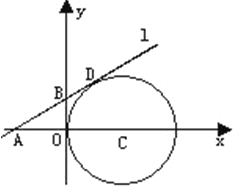
(1)求∠CAD的度数。
(2)求直线![]() 的解析式。
的解析式。
【答案】(1)30°(2)y=![]() x+
x+![]()
【解析】
试题分析:(1)连接CD,由于直线l为⊙C的切线,故CD⊥AD.C点坐标为(1,0),故OC=1,即⊙C的半径为1,由点A的坐标为(-1,0),可求出∠CAD=30度.作DE⊥AC于E点,则∠CDE=∠CAD=30°;(2)可求出CE=![]() ,点B的坐标为(0,
,点B的坐标为(0, ![]() ).设直线l的函数解析式为y=kx+b,把A,B两点的坐标代入即可求出未知数的值从而求出其解析式.
).设直线l的函数解析式为y=kx+b,把A,B两点的坐标代入即可求出未知数的值从而求出其解析式.
试题解析:(1)连接CD,∵直线![]() 为⊙C的切线,∴CD⊥AD。∵C点坐标为(1,0),∴OC=1,即⊙C的半径为1,∴CD=OC=1。
为⊙C的切线,∴CD⊥AD。∵C点坐标为(1,0),∴OC=1,即⊙C的半径为1,∴CD=OC=1。
又∵点A的坐标为(-1,0),∴AC=2,∴∠CAD=30°。
(2)作DE⊥AC于E点,则∠CDE=∠CAD=30°,∴CE=![]() ,
,
![]() ,∴OE=OC-CE=
,∴OE=OC-CE=![]() ,∴点D的坐标为(
,∴点D的坐标为(![]() ,
,![]() )。
)。
设直线![]() 的函数解析式为
的函数解析式为![]() ,则
,则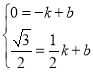
解得k=![]() ,b=
,b=![]() ,
,
∴直线![]() 的函数解析式为y=
的函数解析式为y=![]() x+
x+![]()

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目