题目内容
在实数范围内，把x2+x-2+
分解因式得
- A.（x+2）（x-1）+
- B.（x-2）（x+1）+
- C.（x+）（x+1-）
- D.（x-）（x-1+）
C
分析：由于一、三项符合平方差公式，可分别将一、三和二、四分为一组，然后运用提取公因式法进行二次分解．
解答：原式=（x2-2）+（x+）
=（x+）（x-）+（x+）
=（x+）（x-+1）．
故选C．
点评：主要考查用分组分解法进行因式分解．难点是采用两两分组还是三一分组．本题中一、三项符合平方差公式，应考虑两两分组．
分析：由于一、三项符合平方差公式，可分别将一、三和二、四分为一组，然后运用提取公因式法进行二次分解．
解答：原式=（x2-2）+（x+
）=（x+
）（x-）+（x+）=（x+
）（x-+1）．故选C．
点评：主要考查用分组分解法进行因式分解．难点是采用两两分组还是三一分组．本题中一、三项符合平方差公式，应考虑两两分组．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
在实数范围内，把x2+x-2+
分解因式得（ ）
| 2 |
A、（x+2）（x-1）+
| ||||
B、（x-2）（x+1）+
| ||||
C、（x+
| ||||
D、（x-
|
分解因式得（ ）
）（x+1-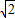
）
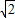）（x-1+
）
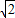分解因式得（ ）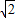
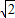
）（x+1-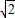
）
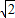）（x-1+
）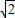