Question

（2007•天水）如图，半径相等的两圆⊙O₁，⊙O₂相交于P，Q两点．圆心O₁在⊙O₂上，PT是⊙O₁的切线，PN是⊙O₂的切线，则∠TPN的大小是（ ）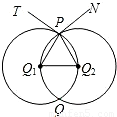

A．90°
B．120°
C．135°
D．150°

Answer 1

【答案】分析：由题意可知△PO₁O₂是等边三角形，所以∠O₁PO₂=60°，又PT是⊙O₁的切线，PN是⊙O₂的切线，可以得到∠TPO₁=∠NPO₂=90°，由此即可求出∠TPN的度数．
解答：解：∵半径相等的两圆⊙O₁，⊙O₂相交于P，Q两点，圆心O₁在⊙O₂上，
∴△PO₁O₂是等边三角形，
∴∠O₁PO₂=60°．
∵PT是⊙O₁的切线，PN是⊙O₂的切线，
∴∠TPO₁=∠NPO₂=90°，
∴∠TPN=360°-90°-90°-60°=120°．
故选B．
点评：本题利用了等边三角形的判定和性质，切线的性质等知识解决问题；注意∠TPN不是∠O₁PO₂的对顶角．