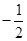题目内容
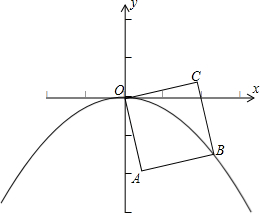 如图,OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )
如图,OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )A、-
| ||||
B、-
| ||||
| C、-2 | ||||
D、-
|
分析:连接OB,过B作BD⊥x轴于D,若OC与x轴正半轴的夹角为15°,那么∠BOD=30°;在正方形OABC中,已知了边长,易求得对角线OB的长,进而可在Rt△OBD中求得BD、OD的值,也就得到了B点的坐标,然后将其代入抛物线的解析式中,即可求得待定系数a的值.
解答: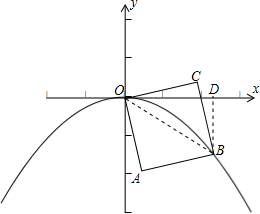 解:如图,连接OB,过B作BD⊥x轴于D;
解:如图,连接OB,过B作BD⊥x轴于D;
则∠BOC=45°,∠BOD=30°;
已知正方形的边长为1,则OB=
;
Rt△OBD中,OB=
,∠BOD=30°,则:
BD=
OB=
,OD=
OB=
;
故B(
,-
),
代入抛物线的解析式中,得:
(
)2a=-
,
解得a=-
;
故选B.
 解:如图,连接OB,过B作BD⊥x轴于D;
解:如图,连接OB,过B作BD⊥x轴于D;则∠BOC=45°,∠BOD=30°;
已知正方形的边长为1,则OB=
| 2 |
Rt△OBD中,OB=
| 2 |
BD=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
故B(
| ||
| 2 |
| ||
| 2 |
代入抛物线的解析式中,得:
(
| ||
| 2 |
| ||
| 2 |
解得a=-
| ||
| 3 |
故选B.
点评:此题主要考查了正方形的性质、直角三角形的性质以及用待定系数法确定函数解析式的方法,能够正确地构造出与所求相关的直角三角形,是解决问题的关键.

练习册系列答案
相关题目

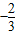
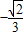
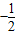
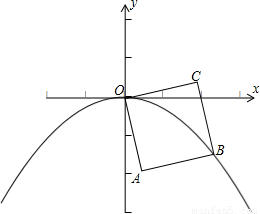
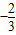
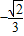
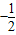
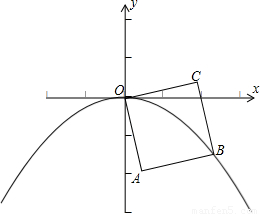
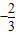
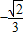
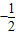
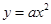 (a<0)的图象上,则a的值为 ( )
(a<0)的图象上,则a的值为 ( ) 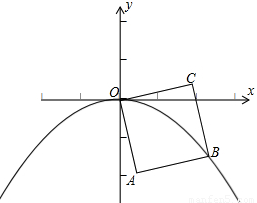
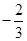 B.
B. C.
C. D.
D.