题目内容
阅读下列材料:解方程
| 1 |
| x-2 |
| x-1 |
| x-2 |
解:方程的两边都乘以x-2,约去分母,得1=x-1-3(x-2).
解这个整式方程,得x=2.
检验:当x=2时,x-2=0,所以2是增根,原方程无解.
请你根据这个方程的特点,用另一种方法解这个方程.
分析:本题考查根据分式方程特点选择不同方法进行解答的能力.因为
和
分母相同,因此可采用同分母分式相加减的方法进行合并,然后去分母解方程.又可以针对
=
的特点进行拆项,计算的方法.具体如下.
| 1 |
| x-2 |
| x-1 |
| x-2 |
| x-1 |
| x-2 |
| x-2+1 |
| x-2 |
解答:解:解法一:∵
=
-3,
∴
-
=-3,
∴
=-3,
∴-1=-3.
∴原方程无解.
解法二:∵
=
-3,
∴
=
-3,
∴
=1+
-3,
∴
=
-2,
∴0=-2.
∴原方程无解.
| 1 |
| x-2 |
| x-1 |
| x-2 |
∴
| 1 |
| x-2 |
| x-1 |
| x-2 |
∴
| -x+2 |
| x-2 |
∴-1=-3.
∴原方程无解.
解法二:∵
| 1 |
| x-2 |
| x-1 |
| x-2 |
∴
| 1 |
| x-2 |
| x-2+1 |
| x-2 |
∴
| 1 |
| x-2 |
| 1 |
| x-2 |
∴
| 1 |
| x-2 |
| 1 |
| x-2 |
∴0=-2.
∴原方程无解.
点评:要根据方程特点灵活选用不同的方法,打破习惯性思维有利于提高解题能力.

练习册系列答案
相关题目
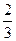 x+1│=1.
x+1│=1.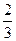 x+1│=1.
x+1│=1.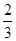 x+1│=1.
x+1│=1.