题目内容
 (2013•海珠区一模)如图,直线y=kx-k+2与抛物线y=
(2013•海珠区一模)如图,直线y=kx-k+2与抛物线y=| 1 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
(1)证明直线y=kx-k+2过定点P,并求出P的坐标;
(2)当k=0时,证明△AQB是等腰直角三角形;
(3)对于任意的实数k,是否都存在一条固定的直线与以AB为直径的圆相切?若存在,请求出此直线的解析式;若不存在,请说明理由.
分析:(1)整理成关于k的形式,然后根据k的系数等于0列式求出x的值,再求出y的值,即可得到定点P的坐标;
(2)先写成直线的解析式,再与抛物线解析式联立求出点A、B的坐标,根据抛物线的解析式求出点Q的坐标,然后利用两点间的距离公式求出AB、AQ、BQ,再根据勾股定理逆定理证明;
(3)设点A(x1,y1)、B(x2,y2),联立直线与抛物线解析式消掉未知数y,得到关于x的一元二次方程,利用根与系数的关系求出AB的长,再求出AB的中点坐标,然后根据AB的长等于AB的中点到x轴的距离的2倍可得以AB为直径的圆与x轴相切.
(2)先写成直线的解析式,再与抛物线解析式联立求出点A、B的坐标,根据抛物线的解析式求出点Q的坐标,然后利用两点间的距离公式求出AB、AQ、BQ,再根据勾股定理逆定理证明;
(3)设点A(x1,y1)、B(x2,y2),联立直线与抛物线解析式消掉未知数y,得到关于x的一元二次方程,利用根与系数的关系求出AB的长,再求出AB的中点坐标,然后根据AB的长等于AB的中点到x轴的距离的2倍可得以AB为直径的圆与x轴相切.
解答:(1)证明:∵y=kx-k+2=k(x-1)+2,
∴当x-1=0,即x=1时,y=2,
故,直线y=kx-k+2过定点P(1,2);
(2)证明:当k=0时,直线y=kx-k+2=2,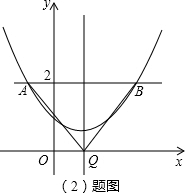
交点A(x1,y1)、B(x2,y2)的坐标符合方程组:
,
解得:
,
,
即A(-1,2),B(3,2),
抛物线y=
x2-
x+
=
(x-1)2+1,
∵抛物线的对称轴与x轴交于点Q,
∴Q(1,0),
∴AB=
=4,
AQ=
=2
,
BQ=
=2
,
∴AB2=AQ2+BQ2,AQ=BQ,
所以,△AQB是等腰直角三角形;
(3)解:存在定直线与以AB为直径的圆相切,此直线即x轴,解析式是y=0.
理由如下:交点A(x1,y1)、B(x2,y2)的坐标符合方程组:
,
消掉y得,
x2-(
+k)x+k-
=0,
∵x1+x2=2+4k,x1x2=4k-3,
∴(x1-x2)2=(x1+x2)2-4x1x2=(2+4k)2-4(4k-3)=16k2+16,
(y1-y2)2=k2(x1-x2)2=k2(16k2+16),
∴AB=
=
=4k2+4,
∴以AB为直径的圆的半径为2k2+2,
∵AB的中点是(
,
),
=
=2k+1,
=
-k+2=k(2k+1)-k+2=2k2+2,
∴AB的中点,即以AB为直径的圆的圆心坐标为(2k+1,2k2+2),
∵圆心到x轴的距离刚好等于半径,
∴存在定直线与以AB为直径的圆相切,此直线即x轴,解析式是y=0.
∴当x-1=0,即x=1时,y=2,
故,直线y=kx-k+2过定点P(1,2);
(2)证明:当k=0时,直线y=kx-k+2=2,

交点A(x1,y1)、B(x2,y2)的坐标符合方程组:
|
解得:
|
|
即A(-1,2),B(3,2),
抛物线y=
| 1 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 4 |
∵抛物线的对称轴与x轴交于点Q,
∴Q(1,0),
∴AB=
| (-1-3)2+(2-2)2 |
AQ=
| (-1-1)2+(2-0)2 |
| 2 |
BQ=
| (3-1)2+(2-0)2 |
| 2 |
∴AB2=AQ2+BQ2,AQ=BQ,
所以,△AQB是等腰直角三角形;
(3)解:存在定直线与以AB为直径的圆相切,此直线即x轴,解析式是y=0.
理由如下:交点A(x1,y1)、B(x2,y2)的坐标符合方程组:
|
消掉y得,
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
∵x1+x2=2+4k,x1x2=4k-3,
∴(x1-x2)2=(x1+x2)2-4x1x2=(2+4k)2-4(4k-3)=16k2+16,
(y1-y2)2=k2(x1-x2)2=k2(16k2+16),
∴AB=
| (x1-x2)2+(y1-y2)2 |
| (16k2+16)+k2(16k2+16) |
∴以AB为直径的圆的半径为2k2+2,
∵AB的中点是(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| x1+x2 |
| 2 |
| 2+4k |
| 2 |
| y1+y2 |
| 2 |
| k(x1+x2) |
| 2 |
∴AB的中点,即以AB为直径的圆的圆心坐标为(2k+1,2k2+2),
∵圆心到x轴的距离刚好等于半径,
∴存在定直线与以AB为直径的圆相切,此直线即x轴,解析式是y=0.
点评:本题是二次函数综合题型,主要考查了直线过定点的求解方法,联立两函数解析式求交点的方法两点间的距离公式,勾股定理逆定理的应用,根与系数的关系,直线与圆的位置关系,综合性较强,难度较大,要特别注意两点间的距离公式的应用.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
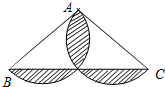 (2013•海珠区一模)如图,在△ABC中,AB=AC=5,CB=8,分别以AB、AC为直径作半圆,则图中阴影部分面积是( )
(2013•海珠区一模)如图,在△ABC中,AB=AC=5,CB=8,分别以AB、AC为直径作半圆,则图中阴影部分面积是( )