题目内容
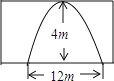
如图是一座抛物线形拱桥，当水面的宽为12m时，拱顶离水面4m，当水面下降2m时，水面的宽为__________m．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
开心蛙状元作业系列答案课时掌控随堂练习系列答案一课一练一本通系列答案浙江之星学业水平测试系列答案题目内容
如图是一座抛物线形拱桥，当水面的宽为12m时，拱顶离水面4m，当水面下降2m时，水面的宽为__________m．
开心蛙状元作业系列答案课时掌控随堂练习系列答案一课一练一本通系列答案浙江之星学业水平测试系列答案
（
为常数），下列说法正确的是（ ）．
，函数与
轴都没有交点
，满足当
时，函数
的值都随
的增大而减小
取不同的值时，二次函数
的顶点始终在同一条直线上
，抛物线
都必定经过唯一定点
，下列说法正确的是（ ）
