��Ŀ����
��ͼ������ABCD��ƽ��ֱ������ϵ�У��ϵ�ADƽ����x�ᣬ�µ�BC��y���ڵ�E����C��4��-2������D��1��2����BC=9��sin��ABC=| 4 |
| 5 |
��1����ֱ��AB�Ľ���ʽ��
��2������H������Ϊ��-1��-1��������G��B��������1����λ/����ٶ�����BC����C���˶�����G�������B���C�غϣ������HGE�����S��S��0���涯��G���˶�ʱ��t����仯�ĺ�����ϵʽ��д���Ա���t���ȡֵ��Χ����
��3���ڣ�2���������£���t��=
| 7 |
| 2 |
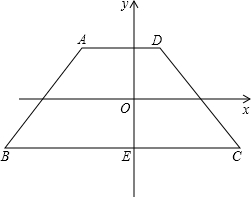
��������1����AF��BC����֪��C����������BC=9��CE=4��BE=5����֪����B��C������Ȼ���������Ǻ����������A�����꣮
��ֱ��AB�Ľ���ʽΪy=kx+b������֪���������������ʽ��
��2������Ҫ������������ۣ����ȵ�G���߶�BE���Ҳ����E�غϣ��ɵ�GE=5-t�䣬S=��5-t�䣩��1��
��
��G���߶�CE���Ҳ����E�غϣ���ʱ��GE=t��-5��S=��t��-5����1��
���ֱ�����Ա�����ȡֵ��Χ���ɣ�
��3����ͼ�����GE�ij����G�������ɵõ�N�����꣮����M������HF��ʱ��������������ۣ�
����P�˶���P1ʱ����P1HM=��HNE������P1��ƽ����y���ֱ�ߣ�֤����P1Q1H�ס�HEN��
=
��Ȼ�����t1��ֵ��
����P�˶�����P2ʱ����P2HN=��HNE����ֱ��P2H��x�ύ�ڵ�T��ֱ��HE��x���ڵ�Q2���ɵá�Q2TH�ס�EHN������
=
���Q2T�ij��Լ���T�����꣮���ֱ��HT�Ľ���ʽ�����t2��ֵ��
����P�˶�����P3ʱ����P3HM1=��HNE������P3��ƽ����y���ֱ��P3Q3����ֱ��HE�ڵ�Q3��ͬ1���t�����ꣻ
����P�˶���P4ʱ����P4HM1=��HNE����֤��P4HE�ա�THQ2�����t��ֵ��
��ֱ��AB�Ľ���ʽΪy=kx+b������֪���������������ʽ��
��2������Ҫ������������ۣ����ȵ�G���߶�BE���Ҳ����E�غϣ��ɵ�GE=5-t�䣬S=��5-t�䣩��1��
| 1 |
| 2 |
��G���߶�CE���Ҳ����E�غϣ���ʱ��GE=t��-5��S=��t��-5����1��
| 1 |
| 2 |
��3����ͼ�����GE�ij����G�������ɵõ�N�����꣮����M������HF��ʱ��������������ۣ�
����P�˶���P1ʱ����P1HM=��HNE������P1��ƽ����y���ֱ�ߣ�֤����P1Q1H�ס�HEN��
| P1Q1 |
| Q1H |
| HE |
| EN |
����P�˶�����P2ʱ����P2HN=��HNE����ֱ��P2H��x�ύ�ڵ�T��ֱ��HE��x���ڵ�Q2���ɵá�Q2TH�ס�EHN������
| Q2T |
| Q2H |
| EH |
| EN |
����P�˶�����P3ʱ����P3HM1=��HNE������P3��ƽ����y���ֱ��P3Q3����ֱ��HE�ڵ�Q3��ͬ1���t�����ꣻ
����P�˶���P4ʱ����P4HM1=��HNE����֤��P4HE�ա�THQ2�����t��ֵ��
���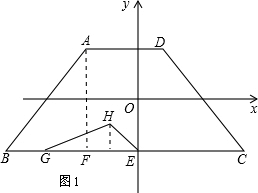 �⣺��1����ͼ1����A��AF��BC��
�⣺��1����ͼ1����A��AF��BC��
��C��4��-2������CE=4��
��BC=9����BE=5��
��B��-5��-2����
��D��1��2������AF=4��
��sin��ABC=
����BF=3��
��A��-2��2����
��ֱ��AB�Ľ���ʽΪy=kx+b��
��
����
��
��ֱ��AB�Ľ���ʽΪy=
x+
��
��2����ͼ1�������⣺
���һ��G���߶�BE���Ҳ����E�غϣ�
��GE=5-t�䣬
S=��5-t�䣩��1��
=
-
t����
�������G���߶�CE���Ҳ����E�غϣ�
��GE=t��-5
S=��t��-5����1��
=
t��-
��
���һ�е��Ա�����ȡֵ��Χ��0��t�䣼5��
������е��Ա�����ȡֵ��Χ��5��t���9��
��3����ͼ2��
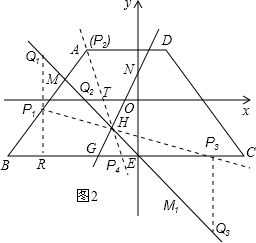 ��t��=
��t��=
��ʱ��GE=5-
=
��G��-
��-2����ֱ��GH����ʽΪy=2x+1��
��N��0��1����
����M������HE��ʱ�������������
���һ������P�˶���P1ʱ����P1HM=��HNE��
����P1��ƽ����y���ֱ�ߣ���ֱ��HE�ڵ�Q1����BC�ڵ�R��
��BP1=t��sin��ABC=
���ɵ�BR=
t1��P1R=
t1��
��RE=Q1R=5-
t1��
��P1Q1=5-
t1��
��Q1H=
(4-
t1)��
�ɡ�P1Q1H�ס�HEN��
=
��
��t1=
��
�൱t1=
ʱ����P1HM=��HNE��
�����������P�˶�����P2ʱ��
��ֱ��P2H��x�ύ�ڵ�T��ֱ��HE��x���ڵ�Q2��
��ʱ����Q2TH�ס�EHN
��
=
���Q2T=
��T(-
��0)��
��ֱ��HT�Ľ���ʽΪy=-3x-4����ʱֱ��HTǡ�þ�����A��-2��2����
���P2���A�غϣ���BP2=5��
��t2=5��
�൱t2=5��ʱ����P2HM=��HNE��
����M������HE��ʱ����M��Ϊ��M1���������������
�����������P�˶�����P3ʱ����P3HM1=��HNE��
����P3��ƽ����y���ֱ��P3Q3����ֱ��HE�ڵ�Q3���������P1ͬ���ķ�����
��t3=15��
�൱t3=15��ʱ����P3HM1=��HNE��
����ģ�����P�˶���P4ʱ����P4HM1=��HNE��
�ɵá�P4HE�ա�THQ2����P4E=TQ2=
����t4=17
�൱t4=17
��ʱ����P4HM2=��HNE��
������������t=
���t=5���t=15���t=17
��ʱ����PHM=��HNE��
 �⣺��1����ͼ1����A��AF��BC��
�⣺��1����ͼ1����A��AF��BC����C��4��-2������CE=4��
��BC=9����BE=5��
��B��-5��-2����
��D��1��2������AF=4��
��sin��ABC=
| 4 |
| 5 |
��A��-2��2����
��ֱ��AB�Ľ���ʽΪy=kx+b��
��
|
|
��ֱ��AB�Ľ���ʽΪy=
| 4 |
| 3 |
| 14 |
| 3 |
��2����ͼ1�������⣺
���һ��G���߶�BE���Ҳ����E�غϣ�
��GE=5-t�䣬
S=��5-t�䣩��1��
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
�������G���߶�CE���Ҳ����E�غϣ�
��GE=t��-5
S=��t��-5����1��
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
���һ�е��Ա�����ȡֵ��Χ��0��t�䣼5��
������е��Ա�����ȡֵ��Χ��5��t���9��
��3����ͼ2��
 ��t��=
��t��=| 7 |
| 2 |
| 7 |
| 2 |
| 3 |
| 2 |
��G��-
| 3 |
| 2 |
��N��0��1����
����M������HE��ʱ�������������
���һ������P�˶���P1ʱ����P1HM=��HNE��
����P1��ƽ����y���ֱ�ߣ���ֱ��HE�ڵ�Q1����BC�ڵ�R��
��BP1=t��sin��ABC=
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
��RE=Q1R=5-
| 3 |
| 5 |
��P1Q1=5-
| 7 |
| 5 |
��Q1H=
| 2 |
| 3 |
| 5 |
�ɡ�P1Q1H�ס�HEN��
| P1Q1 |
| Q1H |
| HE |
| EN |
��t1=
| 7 |
| 3 |
�൱t1=
| 7 |
| 3 |
�����������P�˶�����P2ʱ��
��ֱ��P2H��x�ύ�ڵ�T��ֱ��HE��x���ڵ�Q2��
��ʱ����Q2TH�ס�EHN
��
| Q2T |
| Q2H |
| EH |
| EN |
| 2 |
| 3 |
| 4 |
| 3 |
��ֱ��HT�Ľ���ʽΪy=-3x-4����ʱֱ��HTǡ�þ�����A��-2��2����
���P2���A�غϣ���BP2=5��
��t2=5��
�൱t2=5��ʱ����P2HM=��HNE��
����M������HE��ʱ����M��Ϊ��M1���������������
�����������P�˶�����P3ʱ����P3HM1=��HNE��
����P3��ƽ����y���ֱ��P3Q3����ֱ��HE�ڵ�Q3���������P1ͬ���ķ�����
��t3=15��
�൱t3=15��ʱ����P3HM1=��HNE��
����ģ�����P�˶���P4ʱ����P4HM1=��HNE��
�ɵá�P4HE�ա�THQ2����P4E=TQ2=
| 2 |
| 3 |
| 2 |
| 3 |
�൱t4=17
| 2 |
| 3 |
������������t=
| 7 |
| 3 |
| 2 |
| 3 |
���������⿼�����һ�κ������ۺ������Լ��ֶκ��������ã������ѶȽϴ���Ӧע��ȫ�������Ŀ��⣮

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 ��
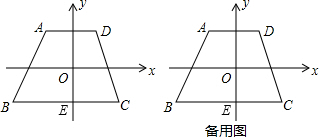
�� ��ʱ����Gֹͣ�˶�����ʱֱ��GH��y�ύ�ڵ�N����һ����P��ʼ��B��������1����λ/����ٶ��������εĸ����˶�һ�ܣ�����B��A��Ȼ����A��D������D��C�������C�ص�B����P���������εĸ������غϣ����趯��P���˶�ʱ��Ϊt�룬��MΪֱ��HE������һ�㣨��M�����H�غϣ����ڵ�P�������˶������У����������ʹ��PHM���HNE��ȵ�t��ֵ��
��ʱ����Gֹͣ�˶�����ʱֱ��GH��y�ύ�ڵ�N����һ����P��ʼ��B��������1����λ/����ٶ��������εĸ����˶�һ�ܣ�����B��A��Ȼ����A��D������D��C�������C�ص�B����P���������εĸ������غϣ����趯��P���˶�ʱ��Ϊt�룬��MΪֱ��HE������һ�㣨��M�����H�غϣ����ڵ�P�������˶������У����������ʹ��PHM���HNE��ȵ�t��ֵ��
 ��
�� ��ʱ����Gֹͣ�˶�����ʱֱ��GH��y�ύ�ڵ�N����һ����P��ʼ��B��������1����λ/����ٶ��������εĸ����˶�һ�ܣ�����B��A��Ȼ����A��D������D��C�������C�ص�B����P���������εĸ������غϣ����趯��P���˶�ʱ��Ϊt�룬��MΪֱ��HE������һ�㣨��M�����H�غϣ����ڵ�P�������˶������У����������ʹ��PHM���HNE��ȵ�t��ֵ��
��ʱ����Gֹͣ�˶�����ʱֱ��GH��y�ύ�ڵ�N����һ����P��ʼ��B��������1����λ/����ٶ��������εĸ����˶�һ�ܣ�����B��A��Ȼ����A��D������D��C�������C�ص�B����P���������εĸ������غϣ����趯��P���˶�ʱ��Ϊt�룬��MΪֱ��HE������һ�㣨��M�����H�غϣ����ڵ�P�������˶������У����������ʹ��PHM���HNE��ȵ�t��ֵ��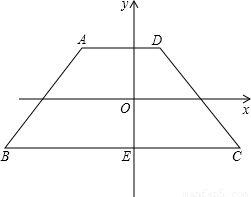
 ��
�� ��ʱ����Gֹͣ�˶�����ʱֱ��GH��y�ύ�ڵ�N����һ����P��ʼ��B��������1����λ/����ٶ��������εĸ����˶�һ�ܣ�����B��A��Ȼ����A��D������D��C�������C�ص�B����P���������εĸ������غϣ����趯��P���˶�ʱ��Ϊt�룬��MΪֱ��HE������һ�㣨��M�����H�غϣ����ڵ�P�������˶������У����������ʹ��PHM���HNE��ȵ�t��ֵ��
��ʱ����Gֹͣ�˶�����ʱֱ��GH��y�ύ�ڵ�N����һ����P��ʼ��B��������1����λ/����ٶ��������εĸ����˶�һ�ܣ�����B��A��Ȼ����A��D������D��C�������C�ص�B����P���������εĸ������غϣ����趯��P���˶�ʱ��Ϊt�룬��MΪֱ��HE������һ�㣨��M�����H�غϣ����ڵ�P�������˶������У����������ʹ��PHM���HNE��ȵ�t��ֵ��