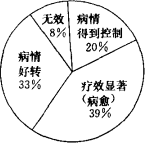
题目内容
(开放性问题)如图所示,AOB是一条直线,∠AOD∶∠DOB=3∶1,OD平分∠COB,求:(1)∠AOC的度数;(2)判断AB与OC的位置关系.

答案:
解析:
提示:
解析:
|
解:(1)因为AOB为一直线,所以∠AOB=∠AOD+∠DOB=180°. 又∠AOD∶∠DOB=3∶1, 可得 又OD平分∠COB,所以∠COD=∠DOB=45°. 所以∠AOC=∠AOD-∠COD=90°. (2)由(1)可知∠AOC=90°,故有AB⊥OC. 精析:判断直线位置关系可求它们的角大小,所以关键是求∠AOC的度数. |
提示:
|
在求角度时,可结合图形,利用角之间的和、差、倍、分关系求度数,如果遇到比例问题,可直接由比例关系求. |

练习册系列答案
相关题目