题目内容
【题目】如图,平面直角坐标系中,直线y= ![]() x+8分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.动点P为CD上一点,PH⊥OA,垂足为H,点Q是点B关于点A的对称点,当BP+PH+HQ值最小时,点P的坐标为_____________________
x+8分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.动点P为CD上一点,PH⊥OA,垂足为H,点Q是点B关于点A的对称点,当BP+PH+HQ值最小时,点P的坐标为_____________________

【答案】(-4,4)
【解析】试题解析:连接PB,CH,HQ,则四边形PHCB是平行四边形,如图,
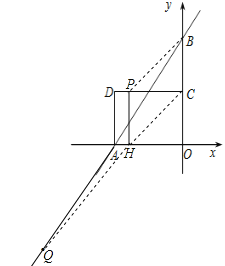
∵四边形PHCB是平行四边形,
∴PB=CH,
∴BP+PH+HQ=CH+HQ+2,
∵BP+PH+HQ有最小值,即CH+HQ+4有最小值,
∴只需CH+HQ最小即可,
∵两点之间线段最短,
∴当点C,H,Q在同一直线上时,CH+HQ的值最小,
过点Q作QM⊥y轴,垂足为M,
∵点Q是点B关于点A的对称点,
∴OA是△BQM的中位线,
∴QM=2OA=12,OM=OB=8,
∴Q(-12,-8),
设直线CQ的关系式为:y=kx+b,
将C(0,4)和Q(-12,-8)分别代入上式得:
![]() ,
,
解得: ![]() ,
,
∴直线CQ的关系式为:y=x+4,
令y=0得:x=-4,
∴H(-4,0),
∵PH∥y轴,
∴P(-4,4).

练习册系列答案
相关题目

