题目内容
 如图,在同一平面内有相同的正方形ABCD和A′B′C′D′,A′与正方形ABCD的中心重合,且正方形A′B′C′D′绕A′转动,则它们重叠部分的面积与正方形ABCD的面积之比是
如图,在同一平面内有相同的正方形ABCD和A′B′C′D′,A′与正方形ABCD的中心重合,且正方形A′B′C′D′绕A′转动,则它们重叠部分的面积与正方形ABCD的面积之比是1:4
1:4
.分析:设A′B′与BC交于M点,A′D′与CD交于N点,根据正方形的性质证明△A′MC≌△A′ND,利用割补法得出S四边形A′MCN=S△A′CD,再根据正方形ABCD与△A′CD的面积关系解题.
解答:解:如图,设A′B′与BC交于M点,A′D′与CD交于N点,
∵∠CA′D=∠MA′N=90°,
∴∠CA′N+∠DA′N=∠MA′C+∠NA′C,
∴∠DA′N=∠MA′C,
又A′D=A′C,∠A′DN=∠A′CM=45°,
∴△A′ND≌△A′MC,
∴S△A′ND=S△A′MC,
∴四边形A′MCN=S△A′CD,
而S△A′CD:S正方形ABCD=1:4,
故答案为:1:4.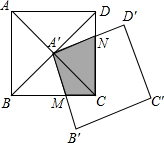
∵∠CA′D=∠MA′N=90°,
∴∠CA′N+∠DA′N=∠MA′C+∠NA′C,
∴∠DA′N=∠MA′C,
又A′D=A′C,∠A′DN=∠A′CM=45°,
∴△A′ND≌△A′MC,
∴S△A′ND=S△A′MC,
∴四边形A′MCN=S△A′CD,
而S△A′CD:S正方形ABCD=1:4,
故答案为:1:4.

点评:本题考查了正方形的性质,运用旋转的性质解题的思想.关键是运用旋转的观点找出两个全等三角形.

练习册系列答案
相关题目
 按要求作图:
按要求作图: 如图,在同一平面内有A、B、C三个点,根据要求画图:
如图,在同一平面内有A、B、C三个点,根据要求画图: 如图,在同一平面内有四个点A、B、C、D
如图,在同一平面内有四个点A、B、C、D