题目内容
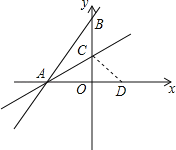
【题目】如图，直线y=
x+4与x轴、y轴分别交于A、B两点，点C在OB上，若将△ABC沿AC折叠，使点B恰好落在x轴上的点D处，则：
（1）线段AB的长是 ．
（2）点C的坐标是 ．
【答案】（1）5（2）（0，1.5）．
【解析】
试题分析：（1）先求出OA、OB，再利用勾股定理即可解决问题．
（2）设OC=x，在Rt△COD中，利用勾股定理列出方程即可解决问题．
解：（1）令x=0，得到y=4，令y=0，得到x=﹣3，
∴A（﹣3，0），B（0，4），
∴OA=3，OB=4，
∵∠AOB=90°，
∴AB=
=
=5，
（2）设OC=x，在Rt△COD中，OD=2，CD=4﹣x，OC=x，
∵CD2=OC2+OD2，
∴（4﹣x）2=x2+22，
解得x=1.5，
∴点C坐标（0，1.5）．
练习册系列答案
相关题目
