题目内容
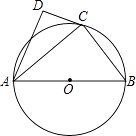
【题目】如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,B、C、E三点共线,连接DC,点F为CD上的一点,连接AF.
(1)若BE平分∠AED,求证:AC=EC;
(2)若∠DAF=∠AEC,求证:BE=2AF.

【答案】(1)见解析;(2)见解析.
【解析】
(1)由等腰直角三角形的性质和角平分线的性质,可得∠ACB=2∠AEC=45°,可得∠AEC=∠EAC=22.5°,可得AC=EC;
(2)过点D作DM∥AC,交AF的延长线于点M,通过证明△ABE≌△DMA,可得AB=DM,AM=BE,通过证明△ACF≌△MDF,可得BE=AM=2AF.
证明:(1)∵△ABC和△ADE均为等腰直角三角形,
∴AB=AC,AE=AD,∠ACB=∠ABC=∠AED=∠ADE=45°,
∵BE平分∠AED,
∴∠AEB=22.5°
∵∠ACB=∠AEC+∠EAC=45°
∴∠AEC=∠EAC=22.5°
∴AC=EC
(2)如图,过点D作DM∥AC,交AF的延长线于点M,
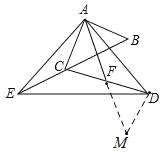
∵∠DAF=∠AEC,且∠AEC+∠EAC=∠ACB=45°
∴∠EAC+∠DAF=45°,且∠DAE=90°,
∴∠CAF=45°
∵AC∥DM,
∴∠CAF=∠DMA=45°
∴∠DMA=∠ABC=45°,且AE=AD,∠AEC=∠DAF,
∴△ABE≌△DMA(AAS)
∴AB=DM,AM=BE,
∴AB=AC=DM,且∠AFC=∠DFM,∠CAF=∠AMD
∴△ACF≌△MDF(AAS)
∴AF=FM
∴AM=2AF=BE

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目