题目内容
（2012•成华区一模）如图，Rt△ABC中，∠C=90°，BC=3cm，AB=5cm．点P从点A出发沿AC以1.5cm/s的速度向点C匀速运动，到达点C后立刻以原来的速度沿CA返回；点Q从点B出发沿BA以1cm/s的速度向点A匀速运动．伴随着P、Q的运动，DE保持垂直平分PQ，且交PQ于点D，交折线PC-CB-BQ于点E．点P、Q同时出发，当点Q到达点A时停止运动，点P也随之停止．设点P、Q运动的时间是t秒（t＞0），则当t=| 25 |
| 11 |
| 40 |
| 23 |
| 25 |
| 11 |
| 40 |
| 23 |
分析：由四边形QBED为直角梯形，分为∠PQB=90°和∠CPQ=90°两种情况，得出三角形相似，利用相似比求出相应t的值即可．
解答：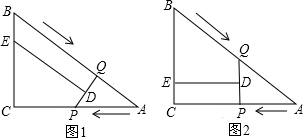
解：在Rt△ABC中，BC=3cm，AB=5cm，
根据勾股定理得：AC=
=4cm，
设P、Q运动t秒时，四边形QBED为直角梯形，
①当∠PQB=90°时，得DE∥QB，
则四边形QBED是直角梯形（如图1），
此时△APQ∽△ABC，
则
=
，即
=
，
解得：t=
；
②当∠CPQ=90°时，得PQ∥BC，
则四边形QBED是直角梯形（如图2），
此时△APQ∽△ACB，
则
=
，即
=
，
解得：t=
，
综上，当点P、Q运动
或
秒时，四边形QBED是直角梯形．
故答案为：
或
解：在Rt△ABC中，BC=3cm，AB=5cm，根据勾股定理得：AC=
| AB2-BC2 |
设P、Q运动t秒时，四边形QBED为直角梯形，
①当∠PQB=90°时，得DE∥QB，
则四边形QBED是直角梯形（如图1），
此时△APQ∽△ABC，
则
| AQ |
| AC |
| AP |
| AB |
| 5-t |
| 4 |
| 1.5t |
| 5 |
解得：t=
| 25 |
| 11 |
②当∠CPQ=90°时，得PQ∥BC，
则四边形QBED是直角梯形（如图2），
此时△APQ∽△ACB，
则
| AQ |
| AB |
| AP |
| AC |
| 5-t |
| 5 |
| 1.5t |
| 4 |
解得：t=
| 40 |
| 23 |
综上，当点P、Q运动
| 25 |
| 11 |
| 40 |
| 23 |
故答案为：
| 25 |
| 11 |
| 40 |
| 23 |
点评：此题考查了四边形综合题，涉及的知识有：相似三角形的判定与性质，直角梯形的性质，利用了分类讨论及数形结合的思想，解题的关键是由直角梯形的直角的可能情况，利用平行线得相似三角形，分类求解．
练习册系列答案
相关题目
（2012•成华区一模）某计算程序编辑如图所示，当输入x=
（2012•成华区一模）某花园内有一块五边形的空地如图所示，为了美化环境，现计划在五边形各顶点为圆心，2m长为半径的扇形区域（阴影部分）种上花草，那么种上花草的扇形区域总面积是
（2012•成华区一模）已知两直线l1、l2分别经过点A（3，0），点B（-1，0），并且当两条直线同时相交于y轴负半轴的点C时，恰好有l1⊥l2，经过点A、B、C的抛物线的对称轴与直线l2交于点K，如图所示．