题目内容
【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点![]() 如果点P在线段BC上以v厘米
如果点P在线段BC上以v厘米![]() 秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动
秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动![]() 若点Q的运动速度为3厘米
若点Q的运动速度为3厘米![]() 秒,则当△BPD与△CQP全等时,v的值为( )
秒,则当△BPD与△CQP全等时,v的值为( )
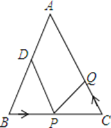
A. 2.5 B. 3 C. 2.25或3 D. 1或5
【答案】C
【解析】分两种情况讨论:①若△BPD≌△CPQ,根据全等三角形的性质,则BD=CQ=6厘米,BP=CP=![]() BC=
BC=![]() ×9=4.5(厘米),根据速度、路程、时间的关系即可求得;②若△BPD≌△CQP,则CP=BD=6厘米,BP=CQ,得出
×9=4.5(厘米),根据速度、路程、时间的关系即可求得;②若△BPD≌△CQP,则CP=BD=6厘米,BP=CQ,得出![]() ,解得:v=3.
,解得:v=3.
∵△ABC中,AB=AC=12厘米,点D为AB的中点,
∴BD=6厘米,
若△BPD≌△CPQ,则需BD=CQ=6厘米,BP=CP=![]() BC=
BC=![]() ×9=4.5(厘米),
×9=4.5(厘米),
∵点Q的运动速度为3厘米/秒,
∴点Q的运动时间为:6÷3=2(s),
∴v=4.5÷2=2.25(厘米/秒);
若△BPD≌△CQP,则需CP=BD=6厘米,BP=CQ,
∴![]() ,
,
解得:v=3;
∴v的值为:2.25或3,
故选:C.

 考前必练系列答案
考前必练系列答案【题目】阅读理解:德国著名数学家高斯被认为是历史上最重要的数学家之一,并有"数学王子"的美誉.高斯从小就善于观察和思考.在他读小学时候就能在课堂上快速的计算出![]() ,今天我们可以将高斯的做法归纳如下:
,今天我们可以将高斯的做法归纳如下:
令![]() ①
①
![]() ②
②
(右边相加100+1=2+99=3+98=…..=100+1共100组)
①+②:有2S=101x100 解得:![]()
(1)请参照以上做法,回答,3+5+7+9+…..+97= ;
请尝试解决下列问题:
如下图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.

(2)填写下表:
层数 | 1 | 2 | 3 | 4 |
该层对应的点数 | 1 | 6 | 12 | 18 |
所有层的总点数的和 | 1 | 7 | 19 |
①写出第n层所对应的点数;(n≥2)
②如果某一层共96个点,求它是第几层;
③写出n层的六边形点阵的总点数.
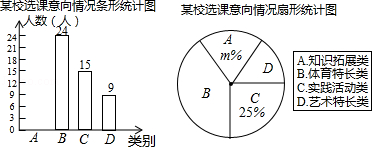
【题目】随着我市社会经济的发展和交通状况的改善,我市的旅游业得到了高速发展![]() 某旅游公司对我市一企业个人旅游年消费情况进行问卷调查
某旅游公司对我市一企业个人旅游年消费情况进行问卷调查![]() 随机抽取部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成如下两幅尚不完整的表和图:
随机抽取部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成如下两幅尚不完整的表和图:
组别 | 个人年消费金额 | 频数 | 频率 |
A |
| 18 |
|
B |
| a | b |
C |
|
|
|
D |
| 24 |
|
E |
| 12 |
|
合计 | c |
| |

根据以上信息解答下列问题:
![]() ________;
________; ![]() ________;
________; ![]() ________;
________;
![]() 补全频数分布直方图;
补全频数分布直方图;
![]() 若这个企业有3000名员工,请你估计个人旅游年消费金额在6000元以上的人数.
若这个企业有3000名员工,请你估计个人旅游年消费金额在6000元以上的人数.