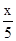题目内容
春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第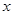 天(
天(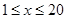 且
且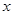 为整数)的捕捞与销售的相关信息如表:
为整数)的捕捞与销售的相关信息如表:
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) | 5-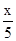 |
| 捕捞量(kg) | 950-10x |
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第
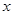 天的收入
天的收入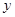 (元)与
(元)与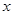 (天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)
(天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)(3)试说明⑵中的函数
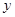 随
随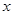 的变化情况,并指出在第几天
的变化情况,并指出在第几天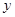 取得最大值,最大值是多少?
取得最大值,最大值是多少?
(1)每天的捕捞量与前一天减少10kg;(2)y=-2x2+40x+14250;(3)第10天,y取得最大值为14450元.
解析试题分析:(1)由图表中的数据可知该养殖场每天的捕捞量比前一天减少10kg;
(2)根据收入=捕捞量×单价-捕捞成本,列出函数表达式;
(3)将实际转化为求函数最值问题,从而求得最大值.
(1)根据捕捞量与天数x的关系:950-10x可知:该养殖场每天的捕捞量与前一天减少10kg;
(2)由题意得y=20(950-10x)-(5-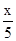 )(950-10x)=-2x2+40x+14250;
)(950-10x)=-2x2+40x+14250;
(3)∵-2<0,y=-2x2+40x+14250=-2(x-10)2+14450,
又∵1≤x≤20且x为整数,
∴当1≤x≤10时,y随x的增大而增大;
当10≤x≤20时,y随x的增大而减小;
当x=10时即在第10天,y取得最大值,最大值为14450.
考点:二次函数的应用
点评:解题的关键是要运用图表中的信息,将实际问题转化为求函数最值问题,从而来解决实际问题.

| 鲜鱼销售单价(元/kg) | 20 | ||
| 单位捕捞成本(元/kg) | 5-
| ||
| 捕捞量(kg) | 950-10x |
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(天)之间的函数关系式?(当天收入=日销售额-日捕捞成本)
(3)试说明(2)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第 天(
天(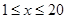 且
且 为整数)的捕捞与销售的相关信息如表:
为整数)的捕捞与销售的相关信息如表:
|
鲜鱼销售单价(元/kg) |
20 |
|
单位捕捞成本(元/kg) |
5- |
|
捕捞量(kg) |
950-10x |
(1)在此期间该养殖场每天的捕捞量与前一天的捕捞量相比是如何变化的 (填“增加”或“减少”了多少kg.)
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第 天的收入
天的收入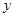 (元)与
(元)与 (天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)
(天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)
(3)试说明⑵中的函数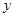 随
随 的变化情况,并指出在第几天
的变化情况,并指出在第几天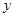 取得最大值,最大值是多少?
取得最大值,最大值是多少?
春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第![]() 天(
天(![]() 且
且![]() 为整数)的捕捞与销售的相关信息如下表:
为整数)的捕捞与销售的相关信息如下表:
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) | 5- |
| 捕捞量(kg) | 950-10x |
⑴ 在此期间该养殖场每天的捕捞量与前一天的捕捞量相比是如何变化的 (填“增加”或“减少”了多少kg.)
⑵ 假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第![]() 天的收入
天的收入![]() (元)与
(元)与![]() (天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)
(天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)
(3) 试说明⑵中的函数![]() 随
随![]() 的变化情况,并指出在第几天
的变化情况,并指出在第几天![]() 取得最大值,最大值是多少?
取得最大值,最大值是多少?
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) | 5-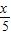 |
| 捕捞量(kg) | 950-10x |
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(天)之间的函数关系式?(当天收入=日销售额-日捕捞成本)
(3)试说明(2)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?