题目内容
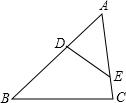如图，若D、E分别为△ABC中AB、AC边上的点，且∠AED=∠B，AD=3，AC=6，DB=5，则AE的长度为
- A.
- B.
- C.
- D.4
D
分析：根据相似三角形的判定首先证出△ADE∽△ACB，然后根据相似三角形的性质得出AE：AB=AD：AC，从而求出AE的长度．
解答：∵∠A=∠A，∠AED=∠B，
∴△ADE∽△ACB，
∴AE：AB=AD：AC，
又∵AD=3，AC=6，DB=5，
∴AB=AD+DB=8，
∴AE=8×3÷6=4．
故选D．
点评：本题主要考查了相似三角形的判定及性质．
有两角对应相等的两个三角形相似．
相似三角形的三边对应成比例．
分析：根据相似三角形的判定首先证出△ADE∽△ACB，然后根据相似三角形的性质得出AE：AB=AD：AC，从而求出AE的长度．
解答：∵∠A=∠A，∠AED=∠B，
∴△ADE∽△ACB，
∴AE：AB=AD：AC，
又∵AD=3，AC=6，DB=5，
∴AB=AD+DB=8，
∴AE=8×3÷6=4．
故选D．
点评：本题主要考查了相似三角形的判定及性质．
有两角对应相等的两个三角形相似．
相似三角形的三边对应成比例．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
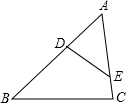如图，若D、E分别为△ABC中AB、AC边上的点，且∠AED=∠B，AD=3，AC=6，DB=5，则AE的长度为（ ）A、
| ||
B、
| ||
C、
| ||
| D、4 |
