题目内容
如图所示,图(1)是一座抛物线型拱桥在建造过程中装模时的设计示意图,拱高为30m,支柱A3B3=50m,5根支柱之间的距离均为15m,将抛物线放在图(2)所示的直角坐标系中.(1)直接写出图(2)中点B1,B3,B5的坐标;
(2)求图(2)中抛物线的函数表达式;
(3)求图(1)中支柱A2B2,A4B4的长度.
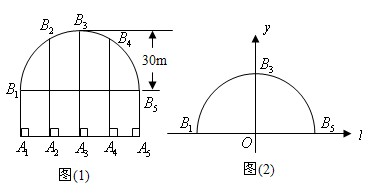
分析:根据建立的坐标系(1)(2)易解决;(3)根据对称性所求的两根支柱长度相同,所以只需求其中一根即可.A2B2=B2的纵坐标+20.
解答:解:
(1)点B1的坐标为(-30,0)
点B3的坐标为(0,30)
点B5的坐标为(30,0)(3分)
(2)由题意知二次函数的对称轴是y轴,设函数的表达式为y=ax2+c,
因为函数过点B3和点B5,
所以
.?
.
∴y=-
x2+30(5分)
(3)当x=±15时,y=-
(±15)2+30=22.5,A2B2=A4B4=22.5+20=42.5(m).(4分)
(1)点B1的坐标为(-30,0)
点B3的坐标为(0,30)
点B5的坐标为(30,0)(3分)
(2)由题意知二次函数的对称轴是y轴,设函数的表达式为y=ax2+c,
因为函数过点B3和点B5,
所以
|
|
∴y=-
| 1 |
| 30 |
(3)当x=±15时,y=-
| 1 |
| 30 |
点评:将实际问题通过建模转化为数学题求解充分体现数学知识的实用性.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
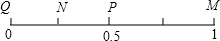 如图所示,下列说法错误的是( )
如图所示,下列说法错误的是( )| A、买一张彩票会中500万元的可能性在图中的大致位置是点M | B、从一副洗匀且背面朝上的扑克牌(大,小王除外)中任意抽取一张牌,抽到的牌面是黑桃的可能性在图中的大致位置是点N | C、掷一枚均匀的正方体形状的骰子,偶数点朝上的可能性在图中的大致位置是点P | D、从分别标有数字1,2,3,4,5的五张纸条中,任意抽取一张,抽到的纸条是“6”的可能性在图中的大致位置是点Q |
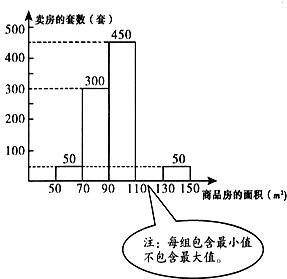 8、现从我市区近期卖出的不同面积的商品房中随机抽取1000套进行统计,并根据结果绘出如图所示的统计图,请结合图中的信息,解答下列问题:
8、现从我市区近期卖出的不同面积的商品房中随机抽取1000套进行统计,并根据结果绘出如图所示的统计图,请结合图中的信息,解答下列问题:
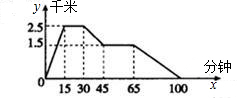 如图所示,图象反映的是:小明从家里跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家,其中x表示时间,y表示小明离家的距离.根据图象回答下列问题:
如图所示,图象反映的是:小明从家里跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家,其中x表示时间,y表示小明离家的距离.根据图象回答下列问题: