题目内容
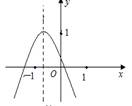
如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,某同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的信息有( )
A. 4个 B.3个 C. 2个 D.1个
【答案】
D.
【解析】
试题分析:(1)根据图示知,该函数图象与x轴有两个交点,所以△=b2﹣4ac>0;故本选项正确;
(2)由图象知,该函数图象与y轴的交点在点(0,1)以下,所以c<1;故本选项错误;
(3)由图示,知对称轴x=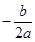 >﹣1;又函数图象的开口方向向下,所以a<0,所以﹣b<﹣2a,即2a﹣b<0,故本选项正确;
>﹣1;又函数图象的开口方向向下,所以a<0,所以﹣b<﹣2a,即2a﹣b<0,故本选项正确;
(4)根据图示可知,当x=1,即y=a+b+c<0,所以a+b+c<0;故本选项正确;
综上所述,我认为其中错误的是(2),共有1个.
故选D.
考点:二次函数图象与系数的关系.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
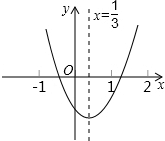 小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面六条信息:
小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面六条信息:①c<0;②abc>0;③a-b+c>0;④2a-3b=0;⑤4a+2b+c>0;⑥一元二次方程ax2+bx+c=0有两异号实根.
你认为其中正确信息的个数有( )
| A、3个 | B、4个 | C、5个 | D、6个 |
 2、从如图所示的二次函数y=ax2+bx+c的图象中,你认为下面不正确的信息是( )
2、从如图所示的二次函数y=ax2+bx+c的图象中,你认为下面不正确的信息是( ) 如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:
如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息: (2012•龙岗区模拟)如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.你认为其中正确的有( )
(2012•龙岗区模拟)如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.你认为其中正确的有( ) 小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:
小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息: