题目内容
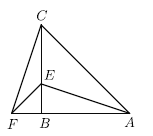
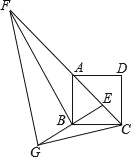
【题目】在正方形ABCD中,对角线AC上取一点E,连接BE,过B作BE的垂线交CA的延长线于F,垂足为B,将△BEF沿BF翻折得到△BGF,连接GC.若tan∠EFG=![]() ,
,![]() ,则GC=_____.
,则GC=_____.
【答案】![]()
【解析】
作GH⊥CF于H,BO⊥CF于O.由tan∠EFG=![]() =
=![]() 可以假设GH=7k,FH=24k,则FG=FE=25k,HE=k,由BG=EB,BO∥GH,推出OH=OE=
可以假设GH=7k,FH=24k,则FG=FE=25k,HE=k,由BG=EB,BO∥GH,推出OH=OE=![]() ,BO=
,BO=![]() BH=
BH=![]() k,在Rt△EGH中,49k2+k2=
k,在Rt△EGH中,49k2+k2=![]() ,求出K即可解决问题.
,求出K即可解决问题.
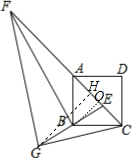
作GH⊥CF于H,BO⊥CF于O,
∵tan∠EFG=![]() =
=![]() ,
,
∴可以假设GH=7k,FH=24k,则FG=FE=25k,HE=k,
∵BG=EB,BO∥GH,
∴OH=OE=![]() ,BO=
,BO=![]() BH=
BH=![]() k,
k,
在Rt△EGH中,49k2+k2=![]() ,
,
∴k=![]() ,
,
∴GH=![]() ,CH=OH+OC=OH+OB=
,CH=OH+OC=OH+OB=![]() ,
,
在Rt△CGH中,CG=![]() =
=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】4月23日为“世界读书日”,每年的这一天,世界100多个国家都会举办各种各样的庆祝和图书宣传活动.我县某书店借此机会决定开展“读书节”活动,为迎接“读书节”制定了活动计划.以下是活动计划书的部分信息:
“读书节”活动计划书 | ||
图书类別 | A类 | B类 |
进价(元/本) | 18 | 12 |
备注 | (1)用不超过16800元购进A、B两类图书共1000本: (2)A类图书不少于600本: | |
(1)陈经理査看计划书时发现:A类图书的标价是B类图书标价的1.5倍,若顾客同样用540元购买图书,能购买A类图书数量比B类图书的数量少10本,请求出A、B两类图书的标价;
(2)经市场调查后,陈经理发现它们高估了“读书节”对图书销售的影响:便调整了销售方案;A类图书每本按标价降低2元销售,B类图书价格不变,那么该书店应如何进货才能获得最大利润?