题目内容
【题目】八(1)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
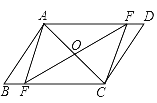
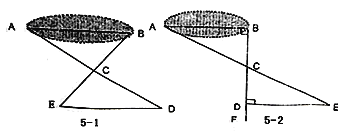
(Ⅰ)如图5-1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;
(Ⅱ)如图5-2,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.
阅读后1回答下列问题:
(1)方案(Ⅰ)是否可行?说明理由.
(2)方案(Ⅱ)是否可行?说明理由.
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是 ;若仅满足∠ABD=∠BDE≠90°, 方案(Ⅱ)是否成立? .
【答案】(1)见解析;(2)见解析;(3)∠ABD=∠BDE=90°,成立.
【解析】
(1)由题意可证明△ACB≌△DCE,AB=DE,故方案(Ⅰ)可行;
(2)由题意可证明△ABC≌△EDC,AB=ED,故方案(Ⅱ)可行;
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是∠ABD=∠BDE;若仅满足∠ABD=∠BDE≠90°,仍可以证明△ABC≌△EDC,则也可得到AB=ED.
(1)在△ACB和△DCE中
∵AC=DC
∠ACB=∠DCE
BC=EC
∴△ACB≌△DCE(SAS)
∴AB=DE,
故方案(Ⅰ)可行;
(2)∵CB⊥AB、CD⊥DE
∴∠ABC=∠EDC=90°
在△ABC和△EDC中
∵∠ABC=∠EDC
BC=DC
∠ACB=∠ECD
∴△ABC≌△EDC (ASA)
∴ED=AB,
故方案(Ⅱ)可行;
(3)作BF⊥AB,ED⊥BF的目的是 作∠ABC=∠EDC=90°;
如果∠ABD=∠BDE≠90°,仍可以利用ASA证明△ABC≌△EDC,则也可得到AB=ED.
故答案为:(1)见解析;(2)见解析;(3)∠ABD=∠BDE=90°,成立.

 阅读快车系列答案
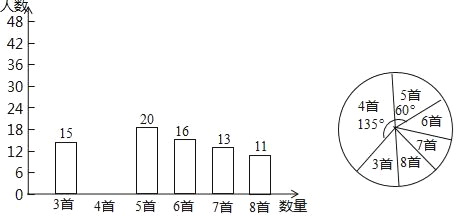
阅读快车系列答案【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根调查结果绘制成的统计图(部分)如图所示.
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 10 | 10 | 15 | 40 | 25 | 20 |
请根据调查的信息
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.