题目内容
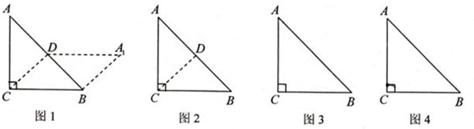
如图,把一个等腰直角三角板AEM放置于矩形ABCD上,AE=BC=13,AB=24.三角板的一个45°角的顶点放在A处,且直角边AE在矩形内部绕点A旋转,在旋转过程中EM与CD交于点F.

(1)如图1,试问线段DF与EF的有何数量关系?并说明理由;
(2)如图1,是否存在△ECB为等腰三角形?若存在,求出DF的长;若不存在,说明理由.继续以下探索:
(3)如图2,以AD为边在矩形内部作正方形ADHI,直角边EM所在的直线交HI于O,交AB于G.设DF=x,OH=y,写出y关于x的函数关系式.

(1)如图1,试问线段DF与EF的有何数量关系?并说明理由;
(2)如图1,是否存在△ECB为等腰三角形?若存在,求出DF的长;若不存在,说明理由.继续以下探索:
(3)如图2,以AD为边在矩形内部作正方形ADHI,直角边EM所在的直线交HI于O,交AB于G.设DF=x,OH=y,写出y关于x的函数关系式.
分析:(1)连接AF.先由矩形的性质得出AD=BC=13,∠D=90°,则AD=AE=13,再利用HL证明△ADF≌△AEF,即可得出DF=EF;
(2)分三种情况进行讨论:①当BE=BC=13时,过E作EP⊥CD于P,延长PE交AB于Q.先由等腰三角形三线合一的性质得出AQ=
AB=12,在Rt△AEQ中,运用勾股定理得出EQ=5,则PE=8,再设DF=x,在Rt△PEF中,运用勾股定理列出关于x的方程,解方程即可;②当EC=BC=13时,连接AC.由AE+EC=13+13<AC=
,根据三角形两边之和大于第三边得出△AEC不存在,即不可能出现EC=BC;③当EC=EB时,过E作EP⊥CD于P,延长PE交AB于Q,先由EC=EB,得出E在BC的垂直平分线上,则PE=EQ=
,再解Rt△AQE,得到∠EAQ=30°,由同角的余角相等得出∠PEF=30°,然后解Rt△PEF即可;
(3)先仿照(1)得出OE=OI,则由OI=HI-OH=13-y,得出OF=13-y+x,然后在Rt△OFH中,运用勾股定理得出OH2+FH2=OF2,即y2+(13-x)2=(13-y+x)2,整理后即可得出y关于x的函数关系式.
(2)分三种情况进行讨论:①当BE=BC=13时,过E作EP⊥CD于P,延长PE交AB于Q.先由等腰三角形三线合一的性质得出AQ=
| 1 |
| 2 |
| 745 |
| 13 |
| 2 |
(3)先仿照(1)得出OE=OI,则由OI=HI-OH=13-y,得出OF=13-y+x,然后在Rt△OFH中,运用勾股定理得出OH2+FH2=OF2,即y2+(13-x)2=(13-y+x)2,整理后即可得出y关于x的函数关系式.
解答: 解:(1)线段DF与EF相等,理由如下:
解:(1)线段DF与EF相等,理由如下:
如图1,连接AF.
∵四边形ABCD是矩形,
∴AD=BC=13,∠D=90°,
∵AE=BC=13,
∴AD=AE=13.
在△ADF与△AEF中,∠D=∠E=90°,
,
∴△ADF≌△AEF(HL),
∴DF=EF;
 (2)分三种情况:
(2)分三种情况:
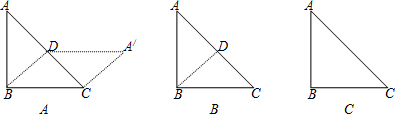
①如图2,当BE=BC=13时,过E作EP⊥CD于P,延长PE交AB于Q,则PQ⊥AB,AQPD是矩形.
∵AE=BC,BE=BC,
∴AE=BE,
∵EQ⊥AB,
∴AQ=QB=
AB=12.
在Rt△AEQ中,∵∠AQE=90°,AE=13,AQ=12,
∴EQ=
=5,
∴PE=PQ-EQ=13-5=8.
设DF=x,则EF=x,FP=12-x,
在Rt△PEF中,∵∠EPF=90°,
∴PE2+FP2=EF2,
 即82+(12-x)2=x2,
即82+(12-x)2=x2,
解得x=
,
∴DF=
;
②如图3,当EC=BC=13时,连接AC.
∵AE=BC=13,EC=BC=13,
∴AE=EC=13.
在Rt△ABC中,∵∠ABC=90°,AB=24,BC=13,
∴AC=
=
,
∵AE+EC=13+13<
,
∴△AEC不存在,
∴不可能出现EC=BC;
 ③如图3,当EC=EB时,过E作EP⊥CD于P,延长PE交AB于Q,则PQ⊥AB,AQPD是矩形.
③如图3,当EC=EB时,过E作EP⊥CD于P,延长PE交AB于Q,则PQ⊥AB,AQPD是矩形.
∵EC=EB,
∴E在BC的垂直平分线上,
∴PE=EQ=
.
∵EQ=
AE,∠AQE=90°,
∴∠EAQ=30°,
∴∠PEF=∠EAQ=90°-∠AEQ=30°,
∴EF=
=
,
∴DF=EF=
;
综上所述,存在△ECB为等腰三角形,此时DF的长
或
;
 (3)如图5,同(1)可证OE=OI,
(3)如图5,同(1)可证OE=OI,
∴OF=OE+EF=OI+DF=OI+x,
∵OI=HI-OH=13-y,
∴OF=13-y+x.
在Rt△OFH中,∵∠OHF=90°,
∴OH2+FH2=OF2,
又∵OH=y,FH=13-x,OF=13-y+x,
∴y2+(13-x)2=(13-y+x)2,
∴y=
.
 解:(1)线段DF与EF相等,理由如下:
解:(1)线段DF与EF相等,理由如下:如图1,连接AF.
∵四边形ABCD是矩形,
∴AD=BC=13,∠D=90°,
∵AE=BC=13,
∴AD=AE=13.
在△ADF与△AEF中,∠D=∠E=90°,
|
∴△ADF≌△AEF(HL),
∴DF=EF;
 (2)分三种情况:
(2)分三种情况:①如图2,当BE=BC=13时,过E作EP⊥CD于P,延长PE交AB于Q,则PQ⊥AB,AQPD是矩形.
∵AE=BC,BE=BC,
∴AE=BE,
∵EQ⊥AB,
∴AQ=QB=
| 1 |
| 2 |
在Rt△AEQ中,∵∠AQE=90°,AE=13,AQ=12,
∴EQ=
| 132-122 |
∴PE=PQ-EQ=13-5=8.
设DF=x,则EF=x,FP=12-x,
在Rt△PEF中,∵∠EPF=90°,
∴PE2+FP2=EF2,
 即82+(12-x)2=x2,
即82+(12-x)2=x2,解得x=
| 26 |
| 3 |
∴DF=
| 26 |
| 3 |
②如图3,当EC=BC=13时,连接AC.
∵AE=BC=13,EC=BC=13,
∴AE=EC=13.
在Rt△ABC中,∵∠ABC=90°,AB=24,BC=13,
∴AC=
| 242+132 |
| 745 |
∵AE+EC=13+13<
| 745 |
∴△AEC不存在,
∴不可能出现EC=BC;
 ③如图3,当EC=EB时,过E作EP⊥CD于P,延长PE交AB于Q,则PQ⊥AB,AQPD是矩形.
③如图3,当EC=EB时,过E作EP⊥CD于P,延长PE交AB于Q,则PQ⊥AB,AQPD是矩形.∵EC=EB,
∴E在BC的垂直平分线上,
∴PE=EQ=
| 13 |
| 2 |
∵EQ=
| 1 |
| 2 |
∴∠EAQ=30°,
∴∠PEF=∠EAQ=90°-∠AEQ=30°,
∴EF=
| PE |
| cos30° |
13
| ||
| 3 |
∴DF=EF=
13
| ||
| 3 |
综上所述,存在△ECB为等腰三角形,此时DF的长
| 26 |
| 3 |
13
| ||
| 3 |
 (3)如图5,同(1)可证OE=OI,
(3)如图5,同(1)可证OE=OI,∴OF=OE+EF=OI+DF=OI+x,
∵OI=HI-OH=13-y,
∴OF=13-y+x.
在Rt△OFH中,∵∠OHF=90°,
∴OH2+FH2=OF2,
又∵OH=y,FH=13-x,OF=13-y+x,
∴y2+(13-x)2=(13-y+x)2,
∴y=
| 26x |
| x+13 |
点评:本题考查了矩形、全等三角形、线段垂直平分线的判定与性质,三角形三边关系定理,等腰三角形、正方形的性质,勾股定理,解直角三角形,综合性较强,有一定难度.运用数形结合与分类讨论思想是解题的关键.

练习册系列答案
相关题目