题目内容
计算下列各式,并且把结果化为只含有正整数指数幂的形式.
(1)(a2b-3)-2?(a-2b3)2
(2)(x5y2z-3)-2
(3)a-2b2•(-2a2b-2)-2÷(a-4b2)
(4) .
.
解:(1)原式=a-4 b6•a-4 b6
=a-8 b12
=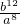 ;
;
(2)原式=x-10 y-4 z 6
= ;
;
(3)原式=a-2 b2• a -4b4•a4b-2
a -4b4•a4b-2
= a-2 b4
a-2 b4
=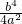 ;
;
(4)原式=( ab-4 c)3
ab-4 c)3
=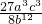 .
.
分析:(1)首先利用积的乘方以及幂的乘方法则计算,然后利用同底数的幂的乘法法则计算,最后根据负指数次幂的意义化成正指数次幂即可;
(2)首先利用积的乘方以及幂的乘方法则计算,然后根据负指数次幂的意义化成正指数次幂即可;
(3)首先利用积的乘方以及幂的乘方法则计算,然后利用同底数的幂的乘法法则计算,最后根据负指数次幂的意义化成正指数次幂即可;
(4)逆用同底数的幂的乘法法则,然后利用幂的乘方法则计算即可.
点评:本题考查同底数幂的除法,负整数指数幂,积的乘方等多个运算性质,需同学们熟练掌握.
=a-8 b12
=
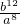 ;
;(2)原式=x-10 y-4 z 6
=
 ;
;(3)原式=a-2 b2•
 a -4b4•a4b-2
a -4b4•a4b-2=
 a-2 b4
a-2 b4=
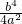 ;
;(4)原式=(
 ab-4 c)3
ab-4 c)3=
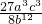 .
.分析:(1)首先利用积的乘方以及幂的乘方法则计算,然后利用同底数的幂的乘法法则计算,最后根据负指数次幂的意义化成正指数次幂即可;
(2)首先利用积的乘方以及幂的乘方法则计算,然后根据负指数次幂的意义化成正指数次幂即可;
(3)首先利用积的乘方以及幂的乘方法则计算,然后利用同底数的幂的乘法法则计算,最后根据负指数次幂的意义化成正指数次幂即可;
(4)逆用同底数的幂的乘法法则,然后利用幂的乘方法则计算即可.
点评:本题考查同底数幂的除法,负整数指数幂,积的乘方等多个运算性质,需同学们熟练掌握.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
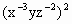 ;
; ;
;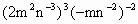 .
.