题目内容
(A类)已知正比例函数y=k1x与反比例函数y=| k2 | x |
(B类)已知函数y=y1+y2,y1与x成正比例,y2与x成反比例,且当x=1时,y=-1;当x=3时,y=5.求y关于x的函数关系式.我选做
分析:(A类)已知正比例函数y=k1x与反比例函数y=
的图象都经过点(2,1),则把(2,1)代入解析式就可以求解;
(B类)首先根据y1与x成正比例,y2与x成反比例,分别建立y1与x,y2与x的函数关系式,从而写出y与x之间的函数关系式,再根据所给的y与x的对应值,列方程组求解.
| k2 |
| x |
(B类)首先根据y1与x成正比例,y2与x成反比例,分别建立y1与x,y2与x的函数关系式,从而写出y与x之间的函数关系式,再根据所给的y与x的对应值,列方程组求解.
解答:解:(A类)
∵正比例函数y=k1x和反比例函数y=
的图象都经过点(2,1),
∴1=2k1,1=
.
∴k1=
,k2=2.
∴这两个函数关系式分别为y=
x和y=
.
(B类)设y1=k1x,y2=
,
则y=k1x+
.
由题意,得
,
解之得
.
∴所求函数的关系式为y=2x-
.
∵正比例函数y=k1x和反比例函数y=
| k2 |
| x |
∴1=2k1,1=
| k2 |
| 2 |
∴k1=
| 1 |
| 2 |
∴这两个函数关系式分别为y=
| 1 |
| 2 |
| 2 |
| x |
(B类)设y1=k1x,y2=
| k2 |
| x |
则y=k1x+
| k2 |
| x |
由题意,得
|
解之得
|
∴所求函数的关系式为y=2x-
| 3 |
| x |
点评:能够熟练运用待定系数法进行求解,特别注意B类中,应当建立y与x之间的函数关系式后,再进一步代入计算.

练习册系列答案
相关题目
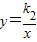 的图象都经过点(2,1),求这两个函数关系式.
的图象都经过点(2,1),求这两个函数关系式.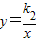 的图象都经过点(2,1),求这两个函数关系式.
的图象都经过点(2,1),求这两个函数关系式.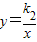 的图象都经过点(2,1),求这两个函数关系式.
的图象都经过点(2,1),求这两个函数关系式.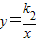 的图象都经过点(2,1),求这两个函数关系式.
的图象都经过点(2,1),求这两个函数关系式.