题目内容
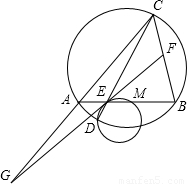
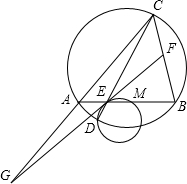 在一圆中,两条弦AB,CD相交于点E,M为线段EB之间的点(不包括E,B).过点D,E,M的圆在点E的切线分别交直线BC,AC于F,G.若
在一圆中,两条弦AB,CD相交于点E,M为线段EB之间的点(不包括E,B).过点D,E,M的圆在点E的切线分别交直线BC,AC于F,G.若| AM |
| AB |
| GE |
| EF |
分析:作辅助线:连接AD,MD,BD,构造相似三角形△CGE∽△BDM,根据相似三角形的对应边成比例求得
=
①;然后再通过相似三角形△CEF∽△AMD的对应边成比例求得
=
②;最后根据①②求得
的值即可.
| GE |
| CE |
| DM |
| MB |
| CE |
| EF |
| AM |
| DB |
| GE |
| EF |
解答: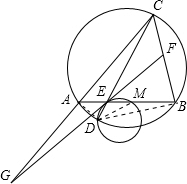 解:连接AD,MD,BD.
解:连接AD,MD,BD.
∵∠DMB=∠CEG,GF是⊙DEM的切线,
∴∠G=∠BDM,
∴△CGE∽△BDM,
∴
=
;①
∴△CEF∽△AMD,
∴
=
;②
①×②得:
=
=
.
 解:连接AD,MD,BD.
解:连接AD,MD,BD.∵∠DMB=∠CEG,GF是⊙DEM的切线,
∴∠G=∠BDM,
∴△CGE∽△BDM,
∴
| GE |
| CE |
| DM |
| MB |
∴△CEF∽△AMD,
∴
| CE |
| EF |
| AM |
| DM |
①×②得:
| GE |
| EF |
| AM |
| MB |
| t |
| 1-t |
点评:本题考查了切线的性质、相似三角形的判定和性质,是基础知识要熟练掌握.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
在一次数学实验探究课中,需要研究同一个圆中两条线段的关系问题,某同学完成了以下部分的记录,单位:cm
(1)请你计算 AE×BE,CE×DE的值,并填入上表相应的位置.
(2)猜想对在同一个圆中,两条线段相交,被交点分成的两条线段的积有什么关系?并试着证明.
(3)利用上述结论,解决问题:AB为⊙O的弦,P是AB上一点,AB=10,PA=4,OP=5,求⊙O的半径R.
| 测量结果 | 第一次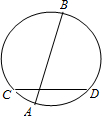 |
第二次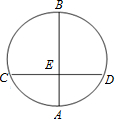 |
第三次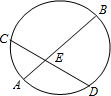 |
| AE | 2.00 | 3.00 | 2.99 |
| BE | 6.01 | 5.00 | 5.00 |
| CE | 3.01 | 3.88 | 3.75 |
| DE | 3.99 | 3.87 | 4.00 |
| AE×BE | |||
| CE×DE |
(2)猜想对在同一个圆中,两条线段相交,被交点分成的两条线段的积有什么关系?并试着证明.
(3)利用上述结论,解决问题:AB为⊙O的弦,P是AB上一点,AB=10,PA=4,OP=5,求⊙O的半径R.
在一次数学实验探究课中,需要研究同一个圆中两条线段的关系问题,某同学完成了以下部分的记录,单位:cm
| 测量结果 | 第一次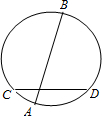 | 第二次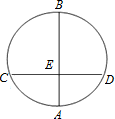 | 第三次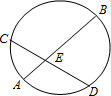 |
| AE | 2.00 | 3.00 | 2.99 |
| BE | 6.01 | 5.00 | 5.00 |
| CE | 3.01 | 3.88 | 3.75 |
| DE | 3.99 | 3.87 | 4.00 |
| AE×BE | |||
| CE×DE |
(2)猜想对在同一个圆中,两条线段相交,被交点分成的两条线段的积有什么关系?并试着证明.
(3)利用上述结论,解决问题:AB为⊙O的弦,P是AB上一点,AB=10,PA=4,OP=5,求⊙O的半径R.
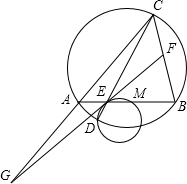 在一圆中,两条弦AB,CD相交于点E,M为线段EB之间的点(不包括E,B).过点D,E,M的圆在点E的切线分别交直线BC,AC于F,G.若
在一圆中,两条弦AB,CD相交于点E,M为线段EB之间的点(不包括E,B).过点D,E,M的圆在点E的切线分别交直线BC,AC于F,G.若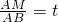 ,求
,求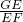 (用t表示).
(用t表示).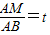 ,求
,求 (用t表示).
(用t表示).