题目内容
在一平行四边形中,有一边的长为6.5,且其对角线长分别为5和12,则其面积为
- A.23.5
- B.39
- C.60
- D.30
D
分析:先运用勾股定理的逆定理判定此平行四边形的两对角线互相垂直,再根据菱形的面积公式即可求出结果.
解答: 解:如图,?ABCD的对角线AC与BD相交于点O,AC=5,BD=12,BC=6.5.
解:如图,?ABCD的对角线AC与BD相交于点O,AC=5,BD=12,BC=6.5.
∵四边形ABCD是平行四边形,
∴OB= BD=6,OC=
BD=6,OC= AC=2.5.
AC=2.5.
在△BOC中,∵OB2+OC2=36+6.25=42.25=BC2,
∴∠BOC=90°,
∴?ABCD是菱形,
∴其面积为: ×AC×BD=
×AC×BD= ×5×12=30.
×5×12=30.
故选D.
点评:本题主要考查了平行四边形的性质,勾股定理的逆定理,菱形的判定及性质,比较简单,运用勾股定理的逆定理得出∠BOC=90°是解题的关键.
分析:先运用勾股定理的逆定理判定此平行四边形的两对角线互相垂直,再根据菱形的面积公式即可求出结果.
解答:
 解:如图,?ABCD的对角线AC与BD相交于点O,AC=5,BD=12,BC=6.5.
解:如图,?ABCD的对角线AC与BD相交于点O,AC=5,BD=12,BC=6.5.∵四边形ABCD是平行四边形,
∴OB=
 BD=6,OC=
BD=6,OC= AC=2.5.
AC=2.5.在△BOC中,∵OB2+OC2=36+6.25=42.25=BC2,
∴∠BOC=90°,
∴?ABCD是菱形,
∴其面积为:
 ×AC×BD=
×AC×BD= ×5×12=30.
×5×12=30.故选D.
点评:本题主要考查了平行四边形的性质,勾股定理的逆定理,菱形的判定及性质,比较简单,运用勾股定理的逆定理得出∠BOC=90°是解题的关键.

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
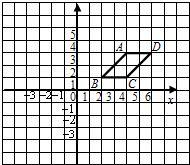 9、如图,在方格纸中,有一平行四边形ABCD,则它关于x轴对称图形的顶点坐标是(2,-1)、(4,-1)、(6,-3)和( )
9、如图,在方格纸中,有一平行四边形ABCD,则它关于x轴对称图形的顶点坐标是(2,-1)、(4,-1)、(6,-3)和( )