题目内容
条 件:如下左图,A、B是直线同旁的两个定点.
问 题:在直线l上确定一点P,使PA+PB的值最小.
方 法:作点A关于直线l的对称点A',连结A'B交l于点P,则PA+PB=A'B的值最小(不必证明).
模型应用:
问 题:在直线l上确定一点P,使PA+PB的值最小.
方 法:作点A关于直线l的对称点A',连结A'B交l于点P,则PA+PB=A'B的值最小(不必证明).
模型应用:

(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连结BD,由正方形对称性可知,B与D关于直线AC对称.连结PE、PB,则PB+PE的最小值是( );
(2)如图2,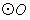 的半径为2,点A、B、C在
的半径为2,点A、B、C在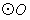 上,
上,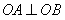 ,
,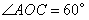 ,P是OB上一动点,求PA+PC的最小值;
,P是OB上一动点,求PA+PC的最小值;
(3)如图3,∠AOB=30°,P是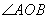 内一点,PO=8,Q,R分别是OA、OB上的动点,求
内一点,PO=8,Q,R分别是OA、OB上的动点,求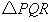 周长的最小值.
周长的最小值.
(2)如图2,
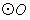 的半径为2,点A、B、C在
的半径为2,点A、B、C在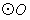 上,
上,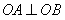 ,
,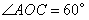 ,P是OB上一动点,求PA+PC的最小值;
,P是OB上一动点,求PA+PC的最小值;(3)如图3,∠AOB=30°,P是
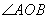 内一点,PO=8,Q,R分别是OA、OB上的动点,求
内一点,PO=8,Q,R分别是OA、OB上的动点,求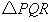 周长的最小值.
周长的最小值. (1)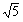 ;
;
(2)延长AO交于点A′,则点A、点A′关于直线OB对称,连接A′C与OB相交于点P,连接AC,因为,OA=OC=2,∠AOC=60°,所以△AOC是等边三角形,所以AC=2,因为AA′=4,,∠ACA′=90°,所以PA+PC=PA′+PC=A′C=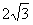 ,即PA+PC的最小值是
,即PA+PC的最小值是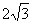 ;
;
(3)分别作P点关于OB、OA的对称点P1,P2,连接P1P2交OA于点Q,交OB于点R,所以OP=OP1=OP2,∠P1OB=∠POB,∠P2OA=∠POA,所以∠P1OP2=2∠AOB=60°,所以△P1OP2是等边三角形,P1P2=OP=8,所以,三角形PQR的周长=PR+PQ+RQ=P1R+P2Q+RQ= P1P2=8,即△PQR的周长的最小值为8
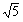 ;
;(2)延长AO交于点A′,则点A、点A′关于直线OB对称,连接A′C与OB相交于点P,连接AC,因为,OA=OC=2,∠AOC=60°,所以△AOC是等边三角形,所以AC=2,因为AA′=4,,∠ACA′=90°,所以PA+PC=PA′+PC=A′C=
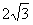 ,即PA+PC的最小值是
,即PA+PC的最小值是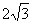 ;
;(3)分别作P点关于OB、OA的对称点P1,P2,连接P1P2交OA于点Q,交OB于点R,所以OP=OP1=OP2,∠P1OB=∠POB,∠P2OA=∠POA,所以∠P1OP2=2∠AOB=60°,所以△P1OP2是等边三角形,P1P2=OP=8,所以,三角形PQR的周长=PR+PQ+RQ=P1R+P2Q+RQ= P1P2=8,即△PQR的周长的最小值为8

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目