题目内容
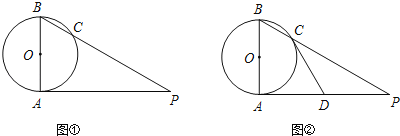
【题目】已知AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C．
（1）如图①，若∠P=35°，求∠ABP的度数；
（2）如图②，若直线CD是⊙O的切线，求证：D为AP的中点．
【答案】（1）55°（2）见解析
【解析】
（1）易证PA⊥AB，再通过解直角三角形求解；
（2）连接OC、AC，证出OC⊥CD，AB⊥AP，根据半径所对应的角相等即可证明CD= AD；根据AB是O的直径，得出∠BCA=90°，再根据两个角相加为90°，即可证明CD= DP，从而得出结论
（1）∵AB是⊙O的直径，AP是⊙O的切线
∴PA⊥AB
∴∠BAP=90°
∵∠P=35°
∴∠ABP=∠BAP-∠P=90°-35°=55°
故答案为：55°
(2)如图，连接OC、AC
∵CD是⊙O的切线
∴OC⊥CD
∴∠1+∠3=90°
∵AP是⊙O的切线
∴AB⊥AP
∴∠2+∠4=90°
∵OA= OC
∴∠1=∠2
∴∠3=∠4
∴ CD= AD
∵AB是O的直径，
∴∠BCA=90°
∴∠DCP+∠3=90°
∠CPA+∠4=90°
∴∠DCP=∠CPA
∴CD= DP
∴CD= DP=AD
∴D为AP的中点
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
