题目内容
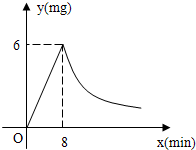
为预防“非典”,某学校对教室采取药熏的方式进行消毒,已知药物燃烧时室内每立方米空气中含药量y(mg)与时间x(min)成正比例,药物燃烧后y与x成反比例,已知药物8min燃烧完,此时室内空气中每立方米的含药量为6mg.(1)研究表明:当空气中每立方米的含药量低于1.6mg时,学生方可进教室,那么从消毒开始,至少需几分钟后,学生才能回教室?
(2)研究表明:当空气中每立方米的含药量不低于3mg,且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?

【答案】分析:已知药物燃烧时室内每立方米空气中含药量y(mg)与时间x(min)成正比例,药物燃烧后y与x成反比例,都过(8,6)点,可求出函数式,把y=1.6代入反比例函数式可求解;把y=3代入正比例函数看看从什么时候开始,代入反比例函数看看到什么时候结束.
解答:解:(1)设正比例函数y=k1x,反比例函数y=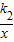 ,都过(8,6)点,
,都过(8,6)点,
6=8k1,k1= ;6=
;6=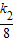 ,k2=48,
,k2=48,
y2=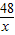 ,
,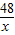 =1.6,x=30;
=1.6,x=30;
(2)3= x,x=4,
x,x=4,
3=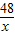 ,
,
x=16,
16-4=12>10,
所以此次消毒有效.
点评:现实生活中存在大量成正比例和反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.然后代入自变量和函数值求相应的解.
解答:解:(1)设正比例函数y=k1x,反比例函数y=
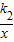 ,都过(8,6)点,
,都过(8,6)点,6=8k1,k1=
 ;6=
;6=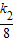 ,k2=48,
,k2=48,y2=
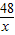 ,
,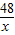 =1.6,x=30;
=1.6,x=30;(2)3=
 x,x=4,
x,x=4,3=
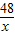 ,
,x=16,
16-4=12>10,
所以此次消毒有效.
点评:现实生活中存在大量成正比例和反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.然后代入自变量和函数值求相应的解.

练习册系列答案
相关题目
 的含药量为6mg.
的含药量为6mg. 的含药量为6mg.
的含药量为6mg.