题目内容
如图,已知抛物y=x2-ax+a+2与x轴交于A、B两点,与y轴交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C.动点P以每秒2个单位长度的速度从点C出发,沿C→D运动.同时、点Q以每秒1个单位长度的速度从点A出发,沿A→B运动.连结PQ、CB.设点P的运动时间为t秒.
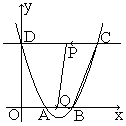
(1)求a的值;
(2)当t为何值时,PQ平行于y轴;
(3)当四边形PQBC的面积等于14时,求t的值.
答案:
解析:
解析:
|
(1)∵D(0,8)在抛物线上,∴a+2=8,∴a=6; (2)当a=6时,抛物线解析式为y=x2-6x+8,当y=8时,x2-6x=0,∴x1=0,x2=6,∴C(6,8),当y=0时,x2-6x+8=0,∴x1=2,x2=4,∴A(2,0),B(4,0),∵CP=2t,AQ=t,∴P(6-2t,8),Q(2+t,0),由6-2t=2+t,得t= (3)SPQIC= |

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目