题目内容
已知:如图1,⊙O与射线MN相切于点M,⊙O的半径为2,AC是⊙O的直径,A与M重合,△ABC是⊙O的内接三角形,且∠C=30°,计算:弦AB=______,
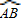 的长度______(结果保留π)
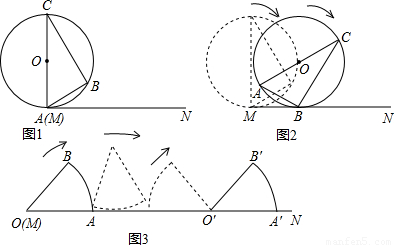
的长度______(结果保留π)探究一:如图2,若⊙O和△ABC沿射线MN方向作无滑动的滚动,
(1)直接写出:点B第一次在射线MN上时,圆心O所走过的路线的长______点B第二次在射线MN上时,圆心O所走过的路线的长______(结果保留π)
(2)过点A、C分别作AD⊥MN于D,CE⊥MN于E,连接OD、OE,小明通过作图猜想:OD与OE相等,你认为小明的猜想正确吗?请说明你的理由
探究二:
如图3,将半径为R、圆心角为50°的扇形纸片AOB,在射线MN的方向作无滑动的滚动至扇形A′O′B′处,则顶点O经过的路线总长为______(用含R的代数式表示,结果保留π).
【答案】分析:计算:利用圆周角定理以及等边三角形的判定得出AB的长,再利用弧长公式得出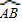 的长度;
的长度;
探究一:(1)利用弧长公式分别求出O点所走过的路线即可;
(2)利用切线的性质定理以及锐角三角函数关系求出OD与OE即可;
探究二:仔细观察顶点O经过的路线可得,顶点O经过的路线可以分为三段,分别求出三段的长,再求出其和即可.
解答: 解:计算:如图1:连接OB,
解:计算:如图1:连接OB,
∵∠C=30°,
∴∠AOB=60°,
又BO=OA,
∴△AOB是等边三角形,
∵⊙O的半径为2,
∴AB=AO=OB=2,
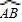 的长度为:
的长度为: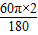 =
= π,
π,
故答案为:2, π;
π;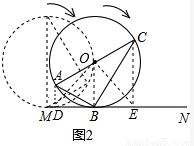
探究一:(1)点B第一次在射线MN上时,圆心O所走过的路线的长为 的长度为:
的长度为: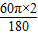 =
= π,
π,
点B第二次在射线MN上时,圆心O所走过的路线的长为: π+2π×2=
π+2π×2=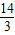 π;
π;
故答案为: π,
π,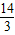 π;
π;
(2)作图如图2所示:
OD=OE,
证明:连接OB,
∵MN与⊙O相切于点B,∴OB⊥MN,
∵∠ACB=30°,
∴∠AOB=60°,AB= AC=2,BC=2
AC=2,BC=2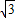 ,
,
∵AO=BO,
∴△AOB是等边三角形,∴∠ABO=60°∴∠ABD=30°
在Rt△ADB中,BD=AB•cos30°=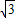
显然∠CBE=60°,
在Rt△BEC中,BE=BC•cos60°=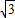 ,
,
∴BD=BE,
∴OD=OE;
探究二:
如图3所示:
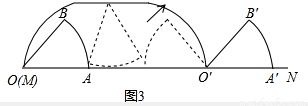
顶点O经过的路线可以分为三段,当弧AB切直线l于点B时,有OB⊥直线l,此时O点绕不动点B转过了90°,滚动距离为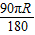 ;
;
第二段:OB⊥直线l到OA⊥直线l,O点绕动点转动,而这一过程中弧AB始终是切于直线l的,所以O与转动点P的连线始终⊥直线l,所以O点在水平运动,此时O点经过的路线长=BA′=AB的弧长=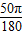 R,
R,
第三段:OA⊥直线l到O点落在直线l上,O点绕不动点A转过了90°,滚动距离为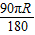 ;
;
所以,O点经过的路线总长S=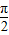 R+
R+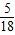 πR+
πR+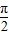 R=
R=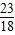 πR.
πR.
故答案为: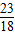 πR.
πR.
点评:此题主要考查了弧长公式的应用以及圆周角定理和锐角三角函数关系等知识,本题关键是理解顶点O经过的路线可得,则顶点O经过的路线总长为三个扇形的弧长.
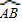 的长度;
的长度;探究一:(1)利用弧长公式分别求出O点所走过的路线即可;
(2)利用切线的性质定理以及锐角三角函数关系求出OD与OE即可;
探究二:仔细观察顶点O经过的路线可得,顶点O经过的路线可以分为三段,分别求出三段的长,再求出其和即可.
解答:
 解:计算:如图1:连接OB,
解:计算:如图1:连接OB,∵∠C=30°,
∴∠AOB=60°,
又BO=OA,
∴△AOB是等边三角形,
∵⊙O的半径为2,
∴AB=AO=OB=2,
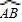 的长度为:
的长度为: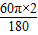 =
= π,
π,故答案为:2,
 π;
π;
探究一:(1)点B第一次在射线MN上时,圆心O所走过的路线的长为
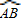 的长度为:
的长度为: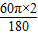 =
= π,
π,点B第二次在射线MN上时,圆心O所走过的路线的长为:
 π+2π×2=
π+2π×2=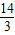 π;
π;故答案为:
 π,
π,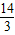 π;
π;(2)作图如图2所示:
OD=OE,
证明:连接OB,
∵MN与⊙O相切于点B,∴OB⊥MN,
∵∠ACB=30°,
∴∠AOB=60°,AB=
 AC=2,BC=2
AC=2,BC=2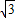 ,
,∵AO=BO,
∴△AOB是等边三角形,∴∠ABO=60°∴∠ABD=30°
在Rt△ADB中,BD=AB•cos30°=
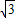
显然∠CBE=60°,
在Rt△BEC中,BE=BC•cos60°=
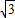 ,
,∴BD=BE,
∴OD=OE;
探究二:
如图3所示:

顶点O经过的路线可以分为三段,当弧AB切直线l于点B时,有OB⊥直线l,此时O点绕不动点B转过了90°,滚动距离为
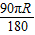 ;
;第二段:OB⊥直线l到OA⊥直线l,O点绕动点转动,而这一过程中弧AB始终是切于直线l的,所以O与转动点P的连线始终⊥直线l,所以O点在水平运动,此时O点经过的路线长=BA′=AB的弧长=
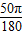 R,
R,第三段:OA⊥直线l到O点落在直线l上,O点绕不动点A转过了90°,滚动距离为
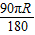 ;
;所以,O点经过的路线总长S=
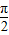 R+
R+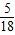 πR+
πR+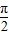 R=
R=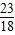 πR.
πR.故答案为:
 πR.
πR.点评:此题主要考查了弧长公式的应用以及圆周角定理和锐角三角函数关系等知识,本题关键是理解顶点O经过的路线可得,则顶点O经过的路线总长为三个扇形的弧长.

练习册系列答案
相关题目
 15、已知:如图,割线AC与圆O交于点B、C,割线AD过圆心O.若圆O的半径是5,且∠DAC=30°,AD=13.求弦BC的长.
15、已知:如图,割线AC与圆O交于点B、C,割线AD过圆心O.若圆O的半径是5,且∠DAC=30°,AD=13.求弦BC的长. ,0)两点,点O1的纵坐标为
,0)两点,点O1的纵坐标为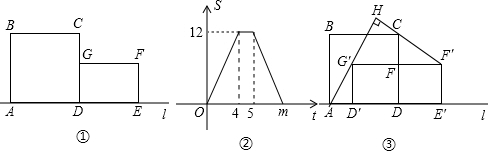
 已知:如图,四边形ABCD与四边形EFGH成中心对称,试画出它们的对称中心,并简要说明理由.
已知:如图,四边形ABCD与四边形EFGH成中心对称,试画出它们的对称中心,并简要说明理由. 已知:如图,直线l1与y轴交点坐标为(0,-1),直线l2与x轴交点坐标为(3,0),两直线交点为P(1,1),解答下面问题:
已知:如图,直线l1与y轴交点坐标为(0,-1),直线l2与x轴交点坐标为(3,0),两直线交点为P(1,1),解答下面问题: