题目内容
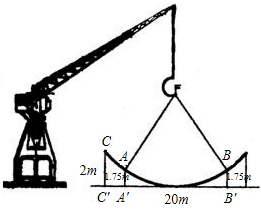 如图:是一抛物线型钢结构,钢结构CD的跨度为20米,拱高CC’=2米.假定用吊车从地面吊起,吊钩位于抛物线顶点O的正上方12.5米点F处,吊绳分别挂在距离地面1.75米的A、B两处,求吊绳的FA、FB的总长.(计算过程中可能用到以下参考数据:4.32=18.49,4.72=22.09,5.32=28.09,5.72=32.49)
如图:是一抛物线型钢结构,钢结构CD的跨度为20米,拱高CC’=2米.假定用吊车从地面吊起,吊钩位于抛物线顶点O的正上方12.5米点F处,吊绳分别挂在距离地面1.75米的A、B两处,求吊绳的FA、FB的总长.(计算过程中可能用到以下参考数据:4.32=18.49,4.72=22.09,5.32=28.09,5.72=32.49)
分析:显然,需建立合适的坐标系.根据题意及抛物线的对称性建立如图所示的坐标系,在Rt△FAH中求FA,根据对称性FB=FA.
解答: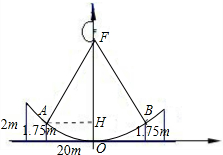 解:如图所示,建立平面直角坐标系,作AH⊥FO于H点,
解:如图所示,建立平面直角坐标系,作AH⊥FO于H点,
设抛物线的解析式为y=ax2,(1分)
∵经过点(10,2),
∴得a=
,(1分)
∴y=
x2(-10≤x≤10),(2分)
当y=1.75时,x=±
,(1分)
FH=12.5-1.75=10.75=
,(1分)
∴AF=
=
=
.(2分)
所以吊绳总长AF+BF=
米(2分).
 解:如图所示,建立平面直角坐标系,作AH⊥FO于H点,
解:如图所示,建立平面直角坐标系,作AH⊥FO于H点,设抛物线的解析式为y=ax2,(1分)
∵经过点(10,2),
∴得a=
| 1 |
| 50 |
∴y=
| 1 |
| 50 |
当y=1.75时,x=±
| ||
| 2 |
FH=12.5-1.75=10.75=
| 43 |
| 4 |
∴AF=
(
|
3
| ||
| 4 |
| 57 |
| 4 |
所以吊绳总长AF+BF=
| 57 |
| 2 |
点评:建立合适的坐标系是数学建模的关键,涉及到计算量的大小及难易程度,所以需认真审题,根据实物特征联系相关数学知识斟酌决定.

练习册系列答案
相关题目
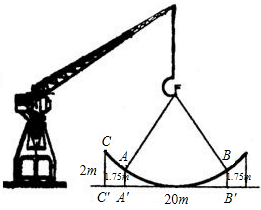 如图:是一抛物线型钢结构,钢结构CD的跨度为20米,拱高CC’=2米.假定用吊车从地面吊起,吊钩位于抛物线顶点O的正上方12.5米点F处,吊绳分别挂在距离地面1.75米的A、B两处,求吊绳的FA、FB的总长.(计算过程中可能用到以下参考数据:4.32=18.49,4.72=22.09,5.32=28.09,5.72=32.49)
如图:是一抛物线型钢结构,钢结构CD的跨度为20米,拱高CC’=2米.假定用吊车从地面吊起,吊钩位于抛物线顶点O的正上方12.5米点F处,吊绳分别挂在距离地面1.75米的A、B两处,求吊绳的FA、FB的总长.(计算过程中可能用到以下参考数据:4.32=18.49,4.72=22.09,5.32=28.09,5.72=32.49)