题目内容
如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D、C.若∠CAB=30°,CD=2,则阴影部分面积是( )

A.  B.
B.  C.
C.  ﹣
﹣ D.
D. 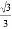 ﹣
﹣
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D、C.若∠CAB=30°,CD=2,则阴影部分面积是( )

A.  B.
B.  C.
C.  ﹣
﹣ D.
D. 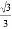 ﹣
﹣
 阅读快车系列答案
阅读快车系列答案