题目内容
已知点A,点B都在双曲线y=
上.点A的坐标为(1,4),点B的横坐标为m(m>2),分别过点A,点B作x轴的垂线,垂足分别为D,C,且AD,OB相交于点E.

(1)求证:△AOE与直角梯形EDCB的面积相等;
(2)延长BO交双曲线y=
于点F,延长AO交双曲线y=
于点H,
①当四边形AFHB为矩形时,求点B的坐标;
②当四边形AFHB的面积为
时,求直线AB的解析式.
| k |
| x |

(1)求证:△AOE与直角梯形EDCB的面积相等;
(2)延长BO交双曲线y=
| k |
| x |
| k |
| x |
①当四边形AFHB为矩形时,求点B的坐标;
②当四边形AFHB的面积为
| 64 |
| 3 |
分析:(1)将A坐标代入反比例函数解析式中求出k的值,确定出反比例解析式,将B的横坐标代入反比例解析式,表示出纵坐标,由A与B的坐标确定出三角形AOD与三角形BOC的面积相等,都减去三角形OED的面积,即可得到三角形AOE与直角梯形EDCB的面积相等;
(2)由对称性得到OA=OH,OB=OF,利用对角线互相平分的四边形为平行四边形得到AFHB为平行四边形,
①当四边形AFHB为矩形时,OA=OB,利用两点间的距离公式列出关于m的方程,求出方程的解得到m的值,即可确定出B的坐标;
②由第一问三角形AOE与直角梯形EDCB的面积相等,都加上三角形AEB的面积,得到三角形AOB的面积与直角梯形ABCD的面积公式,直角梯形上底为B的纵坐标,下底为A的纵坐标,高为B与A横坐标之差,利用梯形面积公式表示出梯形ABCD的面积,即为三角形AOB的面积,而四边形AFBH面积为三角形AOB面积的4倍,由已知AFBH的面积列出关于m的方程,求出方程的解得到m的值,确定出B的坐标,设直线AB解析式为y=kx+b,将A与B的坐标代入求出k与b的值,即可确定出直线AB的解析式.
(2)由对称性得到OA=OH,OB=OF,利用对角线互相平分的四边形为平行四边形得到AFHB为平行四边形,
①当四边形AFHB为矩形时,OA=OB,利用两点间的距离公式列出关于m的方程,求出方程的解得到m的值,即可确定出B的坐标;
②由第一问三角形AOE与直角梯形EDCB的面积相等,都加上三角形AEB的面积,得到三角形AOB的面积与直角梯形ABCD的面积公式,直角梯形上底为B的纵坐标,下底为A的纵坐标,高为B与A横坐标之差,利用梯形面积公式表示出梯形ABCD的面积,即为三角形AOB的面积,而四边形AFBH面积为三角形AOB面积的4倍,由已知AFBH的面积列出关于m的方程,求出方程的解得到m的值,确定出B的坐标,设直线AB解析式为y=kx+b,将A与B的坐标代入求出k与b的值,即可确定出直线AB的解析式.
解答:解:(1)∵点A(1,4)在双曲线y=
上,
∴k=xy=1×4=4,
∵点B也在双曲线y=
上,
∴当x=m时,y=
,即B(m,
),
∵S△AOD=
OD×AD=
×1×4=2,S△BOC=
OC×BC=
×m×
=2,
∴S△AOD=S△BOC,
∴S△AOE+S△ODE=S△ODE+S梯形DEBC,
∴S△AOE=S梯形DEBC;
(2)∵双曲线y=
是关于原点的中心对称图形,
∴OA=OH,OB=OF,
∴四边形ABHF为平行四边形,
①当AH=BF,即OA=OB时,四边形AFHB为矩形,
∴1+42=m2+(
)2,整理得:(m-
)2=9,
解得:m-
=3或m-
=-3,
∵m>2,∴
<1,
∴m-
>0,m-
=-3,舍去,
由m-
=3得,m2-3m-4=0,
解得:m=-1,m=4,
∵m>2,∴m=4,
∴
=1,
此时点B的坐标为(4,1);
②∵四边形AFHB为平行四边形,且对角线AH,BF相交于O点,
∴S平行四边形AFHB=4S△AOB,
由(1)知S△AOE+S△AEB=S△AEB+S梯形DEBC,即S△AOB=S梯形ABCD=
(BC+AD)×CD,
∵AD=4,BC=
,CD=m-1,
∴当四边形AFHB的面积为
时,有4×
(4+
)(m-1)=
,
整理得:3m2-8m-3=0,
解得:m=3,m=-
<2(舍去),
此时点B为(3,
),
设直线AB:y=ax+b,
将A与B的坐标代入得:
,
解得:a=-
,b=
.
则直线AB:y=-
x+
.
| k |
| x |
∴k=xy=1×4=4,
∵点B也在双曲线y=
| 4 |
| x |
∴当x=m时,y=
| 4 |
| m |
| 4 |
| m |
∵S△AOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| m |
∴S△AOD=S△BOC,
∴S△AOE+S△ODE=S△ODE+S梯形DEBC,
∴S△AOE=S梯形DEBC;
(2)∵双曲线y=
| 4 |
| x |
∴OA=OH,OB=OF,
∴四边形ABHF为平行四边形,
①当AH=BF,即OA=OB时,四边形AFHB为矩形,
∴1+42=m2+(
| 4 |
| m |
| 4 |
| m |
解得:m-
| 4 |
| m |
| 4 |
| m |
∵m>2,∴
| 4 |
| m |
∴m-
| 4 |
| m |
| 4 |
| m |
由m-
| 4 |
| m |
解得:m=-1,m=4,
∵m>2,∴m=4,
∴
| 4 |
| m |
此时点B的坐标为(4,1);
②∵四边形AFHB为平行四边形,且对角线AH,BF相交于O点,
∴S平行四边形AFHB=4S△AOB,
由(1)知S△AOE+S△AEB=S△AEB+S梯形DEBC,即S△AOB=S梯形ABCD=
| 1 |
| 2 |
∵AD=4,BC=
| 4 |
| m |
∴当四边形AFHB的面积为
| 64 |
| 3 |
| 1 |
| 2 |
| 4 |
| m |
| 64 |
| 3 |
整理得:3m2-8m-3=0,
解得:m=3,m=-
| 1 |
| 3 |
此时点B为(3,
| 4 |
| 3 |
设直线AB:y=ax+b,
将A与B的坐标代入得:
|
解得:a=-
| 4 |
| 3 |
| 16 |
| 3 |
则直线AB:y=-
| 4 |
| 3 |
| 16 |
| 3 |
点评:此题考查了反比例函数的性质,坐标与图形性质,平行四边形的判定与性质,矩形的判定,以及待定系数法确定函数解析式,是一道多知识的综合题.

练习册系列答案
相关题目
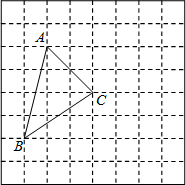 如图,已知△ABC的三个顶点都在格点上,画出△DCF,使得△DCF和△ACB关于点C成中心对称.
如图,已知△ABC的三个顶点都在格点上,画出△DCF,使得△DCF和△ACB关于点C成中心对称.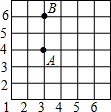 已知三角形的三个顶点都在以下表格的交点上,其中A(3,4),B(3,6),请在表格中确立C点的位置,使S△ABC=3,这样的点C有
已知三角形的三个顶点都在以下表格的交点上,其中A(3,4),B(3,6),请在表格中确立C点的位置,使S△ABC=3,这样的点C有 如图,已知△ABC的三个顶点都在格点上,画出△DCF,使得△DCF和△ACB关于点C成中心对称.
如图,已知△ABC的三个顶点都在格点上,画出△DCF,使得△DCF和△ACB关于点C成中心对称.