题目内容
(12分)公园门票价格规定如下表:
某校初一(1)、(2)两个班共104人去游公园,其中(1)班人数较少,不足50人。经估算,如果两个班都以班为单位购票,则一共应付1240元,问:
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果初一(1)班单独组织去游公园,作为组织者的你将如何购票才最省钱?
| 购票张数 | 1~50张 | 51~100张 | 100张以上 |
| 每张票的价格 | 13元 | 11元 | 9元 |
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果初一(1)班单独组织去游公园,作为组织者的你将如何购票才最省钱?
(1)初一(1)班48人,初一(2)班56人
(2)304元
(3)多买3张。
(2)304元
(3)多买3张。
此应用题考察学生用一元一次方程或二元一次方程组的思路解决实际问题的能力
【第一问】:设初一(1)班人数为x人,则初一(2)班人数为(104-x)人
因为(1)班人数不足50人,所以(1)班每个学生票价为13元,
(2)班人数在51人到100人之间,故(2)班每个学生票价11元。
由关系式“(1)班总钱数+(2)班总钱数 = 1240元”列方程
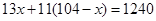 解得
解得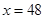
故1班有48个学生,2班有104-48=56个学生
【第二问】:如果两班联合起来,作为一个团体购票,则每张票只要9元,共花费
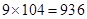 元,可节省
元,可节省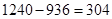 元
元【第三问】如果初一(1)班单独组织去游公园,若按照48人买票,则花费
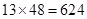 ,若按照51张买,则花费
,若按照51张买,则花费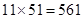 元,
元,所以初一(1)班多买三张票(按51人买)是最省钱的。
评析:本题中第一问是解题关键,而在第一问中,准确读懂表格信息,列出钱数的关系式进而列方程又是重点中的重点。第一问也可以设1班有x人,2班有y人,列二元一次方程组
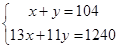 。
。
练习册系列答案
相关题目
 ______.
______. +1=x+2
+1=x+2