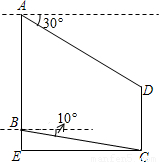
题目内容
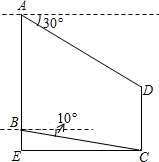 如图,小杰在高层楼A点处,测得多层楼CD最高点D的俯角为30°,小杰从高层楼A处乘电梯往下到达B处,又测得多层楼CD最低点C的俯角为10°,高层楼与多层楼CD之间的距离为CE.已知AB=CE=30米,求多层楼CD的高度.(结果精确到1米)参考数据:
如图,小杰在高层楼A点处,测得多层楼CD最高点D的俯角为30°,小杰从高层楼A处乘电梯往下到达B处,又测得多层楼CD最低点C的俯角为10°,高层楼与多层楼CD之间的距离为CE.已知AB=CE=30米,求多层楼CD的高度.(结果精确到1米)参考数据:| 3 |
分析:过点D作DH⊥AB,垂足为H,在Rt△BEC中,tan∠BCE=
,求得AE、BE,再由在Rt△AHD中,tan∠ADH=
,求出AH,则EH=DC,即为楼高.
| BE |
| CE |
| AH |
| HD |
解答: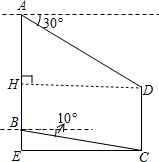 解:过点D作DH⊥AB,垂足为H(1分)
解:过点D作DH⊥AB,垂足为H(1分)
由题意,得:EH=DC,HD=EC=30(1分)∠BCE=10°,∠ADH=30°(1分)
在Rt△BEC中,tan∠BCE=
,
∴tan10°=
(1分),
∴BE=30•tan10°,
∴BE≈5.4(1分),
∵AB=30,
∴AE=35.4(1分),
在Rt△AHD中,tan∠ADH=
,
∴tan30°=
(1分),
∴AH=17.3(1分),
∴EH=DC≈35.4-17.3=18.1≈18(米)(2分),
答:多层楼CD的高度约18米.
 解:过点D作DH⊥AB,垂足为H(1分)
解:过点D作DH⊥AB,垂足为H(1分)由题意,得:EH=DC,HD=EC=30(1分)∠BCE=10°,∠ADH=30°(1分)
在Rt△BEC中,tan∠BCE=
| BE |
| CE |
∴tan10°=
| BE |
| 30 |
∴BE=30•tan10°,
∴BE≈5.4(1分),
∵AB=30,
∴AE=35.4(1分),
在Rt△AHD中,tan∠ADH=
| AH |
| HD |
∴tan30°=
| AH |
| 30 |
∴AH=17.3(1分),
∴EH=DC≈35.4-17.3=18.1≈18(米)(2分),
答:多层楼CD的高度约18米.
点评:本题考查了解直角三角形的应用,俯角仰角问题,是基础知识要熟练掌握.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
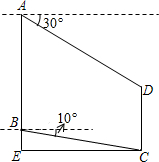 如图,小杰在高层楼A点处,测得多层楼CD最高点D的俯角为30°,小杰从高层楼A处乘电梯往下到达B处,又测得多层楼CD最低点C的俯角为10°,高层楼与多层楼CD之间的距离为CE.已知AB=CE=30米,求多层楼CD的高度.(结果精确到1米)参考数据:
如图,小杰在高层楼A点处,测得多层楼CD最高点D的俯角为30°,小杰从高层楼A处乘电梯往下到达B处,又测得多层楼CD最低点C的俯角为10°,高层楼与多层楼CD之间的距离为CE.已知AB=CE=30米,求多层楼CD的高度.(结果精确到1米)参考数据: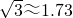 ,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,cot10°≈84.29.
,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,cot10°≈84.29.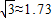 ,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,cot10°≈84.29.
,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,cot10°≈84.29.