题目内容
(2012•南浔区一模)黄金分割比是生活中比较多见的一种长度比值,它能给人许多美感和科学性,我们初中阶段学过的许多几何图形也有着类似的边长比例关系.例如我们熟悉的顶角是36°的等腰三角形,其底与腰之比就为黄金分割比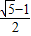 ,底角平分线与腰的交点为黄金分割点.
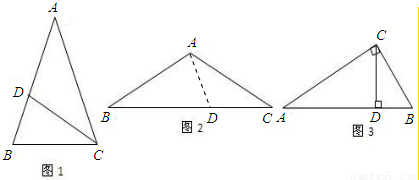
,底角平分线与腰的交点为黄金分割点.(1)如图1,在△ABC中,∠A=36°,AB=AC,∠ACB的角平分线CD交腰AB于点D,请你证明点D是腰AB的黄金分割点;
(2)如图2,在△ABC中,AB=AC,若
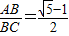 ,则请你求出∠A的度数;
,则请你求出∠A的度数;(3)如图3,如果在Rt△ABC中,∠ACB=90°,CD为AB上的高,∠A、∠B、∠ACB的对边分别为a,b,c.若点D是AB的黄金分割点,那么该直角三角形的三边a,b,c之间是什么数量关系?并证明你的结论.

【答案】分析:(1)根据三角形内角和等于180°,求出∠ABC=∠ACB=72°,再根据CD是∠ACB的角平分线,求出∠ACD=∠BCD=36°,所以△BCD和△ABC是相似的两个等腰三角形,并且AD=BC,根据相似三角形对应边成比例列出比例式整理即可证明;
(2)在BC边上截取BD=AB,连接AD,再根据“AB=AC,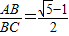 ”分别求出
”分别求出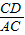 与
与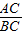 的值都是
的值都是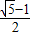 ,所以△ACD∽△ACB,根据相似三角形对应角相等和三角形的一个外角等于和它不相邻的两个内角的和,利用三角形内角和定理列式即可求出∠A的度数;
,所以△ACD∽△ACB,根据相似三角形对应角相等和三角形的一个外角等于和它不相邻的两个内角的和,利用三角形内角和定理列式即可求出∠A的度数;
(3)根据相似三角形对应边成比例分别求出AD、BD的长,再根据AB=AD+BD代入整理即可得到a、b、c之间的关系.
解答:(1)证明:∵在△ABC中,∠A=36°,AB=AC,
∴∠ABC=∠ACB=72°,
又CD是∠ACB的角平分线,
∴∠ACD=∠BCD=36°,
∴∠A=∠DCA,∠BDC=72°,
∴AD=CD=BC,
在△BCD和△BAC中,
∠B=∠B,∠BCD=∠A,
∴△BCD∽△BAC,
∴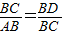 ,
,
∴BC2=AB•BD又BC=AD,(1分)
∴AD2=AB•BD,
∴D是AB的黄金分割点;
(2)解:在底边BC上截取BD=AB,连接AD,
∵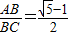 ,AB=AC,
,AB=AC,
∴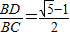 ,
,
∴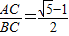 ,
,
∴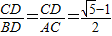 ,
,
∴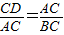 ,
,
又∠C=∠C,
∴△ACD∽△BCA,
∴设∠CAB=∠B=x,
∴∠BAD=∠BDA=2x,
∴x+2x+x+x=180°,
∴x=36°,
∴∠BAC=108°;
(3)解:∵在Rt△ABC中,∠ACB=90°,
CD为AB上的高,
∴△ADC∽△CDB∽△ACB,
′∴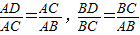
∴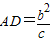 ,
,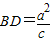 ,(1分)
,(1分)
′∵点D是AB的黄金分割点,
∴AD2=BD•AB,(1分)
∴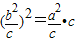 ,
,
该直角三角形的三边a,b,c之间应满足b2=ac.
点评:本题综合性较强,主要利用相似三角形对应边成比例、对应角相等,三角形的外角性质,三角形的内角和定理,熟练掌握各定理和性质并灵活运用是解题的关键.
(2)在BC边上截取BD=AB,连接AD,再根据“AB=AC,
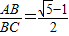 ”分别求出
”分别求出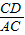 与
与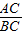 的值都是
的值都是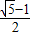 ,所以△ACD∽△ACB,根据相似三角形对应角相等和三角形的一个外角等于和它不相邻的两个内角的和,利用三角形内角和定理列式即可求出∠A的度数;
,所以△ACD∽△ACB,根据相似三角形对应角相等和三角形的一个外角等于和它不相邻的两个内角的和,利用三角形内角和定理列式即可求出∠A的度数;(3)根据相似三角形对应边成比例分别求出AD、BD的长,再根据AB=AD+BD代入整理即可得到a、b、c之间的关系.
解答:(1)证明:∵在△ABC中,∠A=36°,AB=AC,
∴∠ABC=∠ACB=72°,
又CD是∠ACB的角平分线,
∴∠ACD=∠BCD=36°,
∴∠A=∠DCA,∠BDC=72°,
∴AD=CD=BC,
在△BCD和△BAC中,
∠B=∠B,∠BCD=∠A,
∴△BCD∽△BAC,
∴
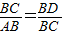 ,
,∴BC2=AB•BD又BC=AD,(1分)
∴AD2=AB•BD,
∴D是AB的黄金分割点;
(2)解:在底边BC上截取BD=AB,连接AD,
∵
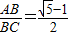 ,AB=AC,
,AB=AC,∴
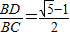 ,
,∴
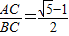 ,
,∴
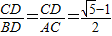 ,
,∴
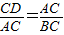 ,
,又∠C=∠C,
∴△ACD∽△BCA,
∴设∠CAB=∠B=x,
∴∠BAD=∠BDA=2x,
∴x+2x+x+x=180°,
∴x=36°,
∴∠BAC=108°;
(3)解:∵在Rt△ABC中,∠ACB=90°,
CD为AB上的高,
∴△ADC∽△CDB∽△ACB,
′∴
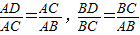
∴
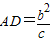 ,
,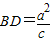 ,(1分)
,(1分)′∵点D是AB的黄金分割点,
∴AD2=BD•AB,(1分)
∴
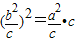 ,
,该直角三角形的三边a,b,c之间应满足b2=ac.

点评:本题综合性较强,主要利用相似三角形对应边成比例、对应角相等,三角形的外角性质,三角形的内角和定理,熟练掌握各定理和性质并灵活运用是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 (2012•南浔区一模)已知:如图,直线l1:y=ax+2b与直线l2:y=cx+2d的交点坐标为(2,3),则a+b+c+d的值是( )
(2012•南浔区一模)已知:如图,直线l1:y=ax+2b与直线l2:y=cx+2d的交点坐标为(2,3),则a+b+c+d的值是( ) (t>0),抛物线y=-x2+bx经过点O和点P.已知矩形ABCD的三个顶点为A(1,0),B(3,0),D(1,3).
(t>0),抛物线y=-x2+bx经过点O和点P.已知矩形ABCD的三个顶点为A(1,0),B(3,0),D(1,3).