题目内容
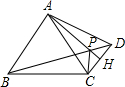 如图AB=BC=CA=AD=
如图AB=BC=CA=AD=| 3 |
| 2 |
分析:首先求得∠APB=60°,然后过A作AE⊥BD于E,即可求得AE的长,继而求出BD的值.
解答: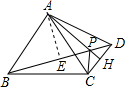 解:∵AB=AD
解:∵AB=AD
∴∠ABD=∠ADB
∵∠ABD+∠ADB+∠BAD=180°
∴∠ADB+
∠BAC+
∠CAD=90°
∵AB=AC=BC
∴∠BAC=60°
∵AC=AD,AH⊥CD
∴∠DAH=
∠CAD
∴∠ADB+∠DAP+30°=90°
∴∠ADB+∠DAP=60°
∵∠DAP+∠ADP=∠APB
∴∠APB=60°
过A作AE⊥BD于E
∴AE=
,
∴AE:AB=
,
∴∠ABE=45°,
∴∠ADB=45°,∠BAD=90°,
∴BD=
AB=
.
故答案为:
.
 解:∵AB=AD
解:∵AB=AD∴∠ABD=∠ADB
∵∠ABD+∠ADB+∠BAD=180°
∴∠ADB+
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=AC=BC
∴∠BAC=60°
∵AC=AD,AH⊥CD
∴∠DAH=
| 1 |
| 2 |
∴∠ADB+∠DAP+30°=90°
∴∠ADB+∠DAP=60°
∵∠DAP+∠ADP=∠APB
∴∠APB=60°
过A作AE⊥BD于E
∴AE=
| 1 |
| 2 |
| 6 |
∴AE:AB=
| ||
| 2 |
∴∠ABE=45°,
∴∠ADB=45°,∠BAD=90°,
∴BD=
| 2 |
| 6 |
故答案为:
| 6 |
点评:本题主要考查了相似三角形的判定与性质,在解题时要能综合应用相似三角形的判定与性质求出线段的长度是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
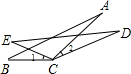 (2013•呼和浩特)如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB.
(2013•呼和浩特)如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB. 如图AB=BC=CA=AD=
如图AB=BC=CA=AD= ,AH⊥CD于H,AP=
,AH⊥CD于H,AP= ,则BD=________.
,则BD=________. ,AH⊥CD于H,AP=
,AH⊥CD于H,AP= ,则BD= .
,则BD= .
 ,AH⊥CD于H,AP=
,AH⊥CD于H,AP=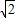 ,则BD= .
,则BD= .