题目内容
如图，线段AB∥线段CD，连接AC，AE平分∠BAC交CD于E，F为AC中点，过F作FG∥AB交AE于G，连接CG，求证：CG平分∠ACD．
证明：由题意得：∠FAG=∠BAG=∠AGF，
∴可得：FG=FC，
∴∠FCG=∠FGC=∠ECG，
从而证得了∠FCG=∠ECG．
∴CG平分∠ACD．
分析：先证AF=FG=FC，从而根据平行线的性质可证得∠FCG=∠ECG，即证得了结论．
点评：本题考查平行线的性质，注意证明一条直线平分一个角要证明分得的两个角相等．
∴可得：FG=FC，
∴∠FCG=∠FGC=∠ECG，
从而证得了∠FCG=∠ECG．
∴CG平分∠ACD．
分析：先证AF=FG=FC，从而根据平行线的性质可证得∠FCG=∠ECG，即证得了结论．
点评：本题考查平行线的性质，注意证明一条直线平分一个角要证明分得的两个角相等．
练习册系列答案
相关题目
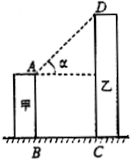14、如图，线段AB、DC分别表示甲、乙两座楼房的高，AB⊥BC，DC⊥BC，两建筑物间距离BC=30米，若甲建筑物高AB=28米，在点A测得D点的仰角α=45°，则乙建筑物高DC=
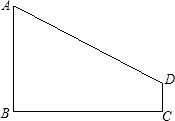已知，如图，线段AB⊥BC，DC⊥BC，垂足分别为点B、C．
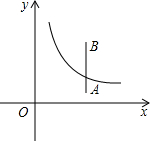（2012•大连二模）如图，线段AB的两个端点的坐标分别是（2，1）、（2，3），函数
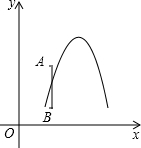如图，线段AB的两个端点的坐标分别是（2，3）、（2，1），函数y=-（x-4）2+k的图象与线段AB有公共点，当该函数图象与y轴的交点最高时，则k的值是（ ）