题目内容
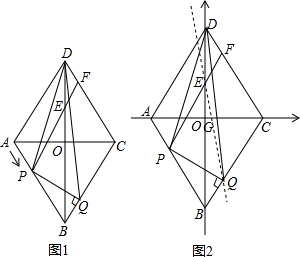
已知:如图1,菱形ABCD的边长为6,∠BAD=120°,对角线相交于O.点P是AB边上一个动点,它从A点出发,以每秒1个长度单位的速度向B点移动,E是OD的中点,连接PE并延长,交CD于F,过点P作PQ⊥BC于Q,连接PEDP、DQ,设移动时间为t(s),DF的长为z,△DPQ的面积为S.
(1)写出使△DEF∽△BEF的条件:______;
(2)求z关于t的函数关系式;
(3)求S关于t的函数关系式,并求出t为何值时,S最大?最大值是多少?
(4)以O为坐标原点,菱形ABCD的对角线所在的直线为坐标轴建立直角坐标系(如图2),直线EQ与x轴的交点为G,当t=2(s)时,①求直线EQ的函数解析式;②求△EOG的外接圆的面积.
(1)解:故答案为:∠DEF=∠BEP,∠FDE=∠PBE.
(2)解:由已知条件得知:PB=6-t,BQ=3- t,
t,
由△DEF∽△BEP,
∴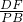 =
=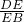 =
= ,
,
x= PB=
PB= (6-t)=-
(6-t)=- t+2.
t+2.
(3)解:S=S△DPB+S△DBQ-P△PBQ,
= (6-t)•6sin60°+
(6-t)•6sin60°+ (3-
(3- t)•6sin60°-
t)•6sin60°- (3-
(3- t)(6-t)sin60°,
t)(6-t)sin60°,
=- t2-
t2- t+9
t+9 .
.
∵t≥0,
∴当t=0时,S最大,最大值是9 .
.
(4)解:①OD=6sin60°=3 ,
,
∴E的坐标是(0, );
);
当t=2秒时,BQ=2,Q的坐标是(1,-2 );
);
设直线EG的解析式是y=kx+b,
把E、G的坐标代入得: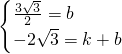 ,
,
解得:k=-
 ,b=
,b= ,
,
∴直线EQ的函数解析式是y=-
 x+
x+ .
.
②把y=0代入得:x= ,
,
∴G的坐标是( ,0),
,0),
由勾股定理得:EG2=EO2+OG2=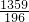 ,
,
∴△EOG的外接圆的面积为π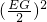 =
=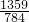 π.
π.
分析:(1)根据相似三角形的判定求出即可;
(2)求出PB、BQ,根据△DEF∽△BEP,得出比例式,代入求出即可;
(3)根据S=S△DPB+S△DBQ-P△PBQ和三角形的面积公式代入求出即可,根据二次函数的顶点式,求出最大值即可;
(4)求出E、G的坐标,用待定系数法求出直线ED即可;根据直线EG的解析式求出与x轴的交点坐标,根据勾股定理求出EG即可.
点评:本题综合考查了二次函数的最值,用待定系数法求出一次函数的解析式,勾股定理,相似三角形的性质和判定,菱形的性质,三角形的外接圆等知识点的运用,此题综合性比较强,有一定的难度,综合运用性质进行推理和计算是解此题的关键.
(2)解:由已知条件得知:PB=6-t,BQ=3-
 t,
t,由△DEF∽△BEP,
∴
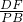 =
=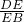 =
= ,
,x=
 PB=
PB= (6-t)=-
(6-t)=- t+2.
t+2.(3)解:S=S△DPB+S△DBQ-P△PBQ,
=
 (6-t)•6sin60°+
(6-t)•6sin60°+ (3-
(3- t)•6sin60°-
t)•6sin60°- (3-
(3- t)(6-t)sin60°,
t)(6-t)sin60°,=-
 t2-
t2- t+9
t+9 .
.∵t≥0,
∴当t=0时,S最大,最大值是9
 .
.(4)解:①OD=6sin60°=3
 ,
,∴E的坐标是(0,
 );
);当t=2秒时,BQ=2,Q的坐标是(1,-2
 );
);设直线EG的解析式是y=kx+b,
把E、G的坐标代入得:
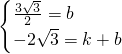 ,
,解得:k=-

 ,b=
,b= ,
,∴直线EQ的函数解析式是y=-

 x+
x+ .
.②把y=0代入得:x=
 ,
,∴G的坐标是(
 ,0),
,0),由勾股定理得:EG2=EO2+OG2=
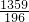 ,
,∴△EOG的外接圆的面积为π
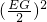 =
=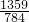 π.
π.分析:(1)根据相似三角形的判定求出即可;
(2)求出PB、BQ,根据△DEF∽△BEP,得出比例式,代入求出即可;
(3)根据S=S△DPB+S△DBQ-P△PBQ和三角形的面积公式代入求出即可,根据二次函数的顶点式,求出最大值即可;
(4)求出E、G的坐标,用待定系数法求出直线ED即可;根据直线EG的解析式求出与x轴的交点坐标,根据勾股定理求出EG即可.
点评:本题综合考查了二次函数的最值,用待定系数法求出一次函数的解析式,勾股定理,相似三角形的性质和判定,菱形的性质,三角形的外接圆等知识点的运用,此题综合性比较强,有一定的难度,综合运用性质进行推理和计算是解此题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
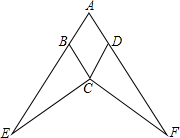 已知:如图,在菱形ABCD中,分别延长AB、AD到E、F,使得BE=DF,连接EC、FC.
已知:如图,在菱形ABCD中,分别延长AB、AD到E、F,使得BE=DF,连接EC、FC. 19、已知:如图,在菱形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F.
19、已知:如图,在菱形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F. 已知:如图,在菱形ABCD中,E为BC边上一点,∠AED=∠B.
已知:如图,在菱形ABCD中,E为BC边上一点,∠AED=∠B. (2013•东城区二模)已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E.
(2013•东城区二模)已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E. (2013•贵阳)已知:如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.
(2013•贵阳)已知:如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.